Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x là chữ số hàng chục, y là chữ số hàng đơn vị.
Điều kiện: x, y ∈N*, 0 < x ≤ 9; 0 < y ≤ 9
Vì hai lần chữ số hàng chục lớn hơn 5 lần chữ số hàng đơn vị là 1 nên ta có: 2x – 5y = 1
Vì chữ số hàng chục chia cho chữ số hàng đơn vị được thương là 2 và dư cũng là 2 nên ta có: x = 2y + 2
Ta có hệ phương trình:
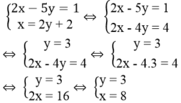
Giá trị của x và y thỏa mãn điều kiện bài toán.
Vậy số cần tìm là 83.

Gọi chữ số hàng chục của số cần tìm là x,chữ số hàng đơn vị là y \(\left(x,y\in N;0< x,y\le9\right)\)
Vì 2 lần cs hàng chục lớn hơn 5 lần cs hàng đơn vị là 1 nên ta có: 2x-5y=1 (1)
Cs hàng chục chia cho cs hàng đơn vị được thương là 2,dư 2. Ta có pt: x=2y+2 <=> x-2y=2 (2)
Từ (1),(2) ta có hpt: \(\hept{\begin{cases}2x-5y=1\\x-2y=2\end{cases}}\)
Giải hệ ta đc: x=8,y=3 (TMĐK)
Vậy số cần tìm là 83

Bài 1:
Tổng số phần bằng nhau: 8+1=9(phần)
Số bé là: 72:9 x 1 = 8
Số lớn là: 8 x 8 = 64
Đ.số:2 số đó là 8 và 64

Gọi chữ số hàng chục là : x ; chữ số hàng đơn vị là : y . Trong đó { \(x,y\in N\); \(x\ne0\)}
Số đó có dạng : \(\overline{xy}\)
Vì chữ số hàng chục lớn hơn chữ số hàng đơn vị là 2 , nên ta có phương trình :
x - y = 2 (1)
Vì nếu lấy số đó chia cho tổng các chữ số của nó thì được thương là 6 dư 2 nên :
\(\overline{xy}=\left(x+y\right).6+1\)
\(\Leftrightarrow10.x+y=6x+6y+1\)
\(\Leftrightarrow4x-5y=1\)(2)
Từ (1) và (2) ta được hệ phương trình :
\(\hept{\begin{cases}x-y=2\\4x-5y=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}4x-4y=8\\4x-5y=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=7\\4x-5.7=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y=7\\x=9\end{cases}}\)
Vậy số cần tìm là : 97

Gọi số đó là abc
Có a=1; b=c-2; 2b-c=4 => 2c - 4 - c=4 <=> c=8 => b=c-2=8-2=6
Vậy số đó là 186