Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tọa đô giao của (d1) và (d2) là:
2x-y=-3 và 15x+3y=-5
=>x=-2/3; y=5/3
Thay x=-2/3 và y=5/3 vào (d3), ta được:
\(3\cdot a\cdot\dfrac{-2}{3}-3\cdot\dfrac{5}{3}+4a+9=0\)
=>-2a-5+4a+9=0
=>2a+4=0
=>a=-2

*Đường thẳng ( d 1 ): 5x – 2y = c đi qua điểm A(5; -1) nên tọa độ điểm A nghiệm đúng phương trình đường thẳng.
Ta có: 5.5 – 2.(-1) = c ⇔ 25 + 2 = c ⇔ c = 27
Phương trình đường thẳng ( d 1 ): 5x – 2y = 27
*Đường thẳng ( d 2 ): x + by = 2 đi qua điểm B(-7; 3) nên tọa độ điểm B nghiệm đúng phương trình đường thẳng.
Ta có: -7 + 3b = 2 ⇔ 3b = 9 ⇔ b = 3
Phương trình đường thẳng ( d 2 ): x + 3y = 2
*Tọa độ giao điểm của (
d
1
) và (
d
2
) là nghiệm của hệ phương trình:![]()
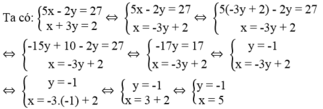
Vậy tọa độ giao điểm của ( d 1 ) và ( d 2 ) là (5; -1).

a, Vì A(1;-3) năm trên đường thẳng (d) khi tọa độ điểm B thỏa mãn phương trình đường thẳng (d)
Thay x = 1 ; y = -3 vào (d) phương trình tương đương
\(-3=5-3m+1\Leftrightarrow4-3x=-3\Leftrightarrow-3x=-7\Leftrightarrow x=\frac{7}{3}\)
b ; c thiếu đề
Bài 2 :
Vì y = x + 5 có tung độ là 2
=> y = 2 + 5 = 7
Vậy y = ( 2m - 5 )x - 5m đi qua đường thẳng y = x + 5 A( 2 ; 7 )
Thay x = 2 ; y = 7 vào y = ( 2m - 5 )x - 5m ta được :
\(7=\left(2m-5\right)2-5m\Leftrightarrow4m-10-5m=7\Leftrightarrow-m=17\Leftrightarrow m=-17\)
Lời giải:
Gọi PTĐT cần tìm có dạng $(\Delta)$: $y=ax+b$ $(a,b\in\mathbb{R}$)
PT hoành độ giao điểm của 2 đường thẳng $(d_1); (d_2)$ là:
\(y=3x-5=-x+4\)
\(\Rightarrow x=\frac{9}{4}\Rightarrow y=\frac{7}{4}\)
Vậy giao điểm của $(d_1); (d_2)$ là $B(\frac{9}{4}, \frac{7}{4})$
Vì $A,B\in (\Delta)$ nên:
\(\left\{\begin{matrix} \frac{-5}{2}=a.\frac{7}{3}+b\\ \frac{7}{4}=a.\frac{9}{4}+b\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=-51\\ b=\frac{233}{2}\end{matrix}\right.\)
\(\Rightarrow (\Delta): y=-51x+\frac{233}{2}\)