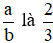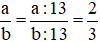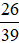Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: 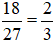
Vậy phân số tối giản của phân số
Mà ƯCLN(a ; b) = 13 nên ta có:
a : 13 = 2 ⇒ a = 26.
b : 13 = 3 ⇒ b = 39.
Vậy phân số cần tìm là
Ta có: 18/27=2/3 là phân số tối giản.
Vậy phân số tối giản của phân số a/b=2/3
Mà ƯCLN(a ; b) = 13 nên ta có: a/b=a:13/b:13=2/3
a : 13 = 2 ⇒ a = 26.
b : 13 = 3 ⇒ b = 39.
Vậy phân số cần tìm là 26/39


\(\dfrac{-5}{9}\)=\(\dfrac{-45}{b}\)
⇒ b= [9. (-45)] : -5
⇒ b= -405 : -5
⇒ b= 81
⇒ \(\dfrac{-45}{81}\)
\(\dfrac{a}{27}\)= \(\dfrac{-5}{9}\)
⇒ a= [ 27 .(-5) ] : 9
⇒ a= -135 : 9
⇒ a= -15
⇒ \(\dfrac{-15}{27}\)
⇒ \(\dfrac{-15}{27}\)=\(\dfrac{-5}{9}\)=\(\dfrac{-45}{81}\)
\(\dfrac{a}{27}=\dfrac{-5}{9}=\dfrac{-45}{b}\)
⇒\(a=\dfrac{-5.27}{9}=-15\)
⇒\(b=\dfrac{-45.9}{5}=-81\)

Đặt 8768903214 = a
7698032145 = b
=> A = a / b
B = a+1 / b+2
Ta có A = a / b
=> A = a(b+2) / b(b+2)
=> A = ab + 2a / b(b+2)
B = a+1 / b+2
=> B = (a+1)b / b(b+2)
=> B = ab+b / b(b+2)
Mà 8768903214 = a
7698032145 = b
=> 2a > b
=> ab + 2a > ab +b
=> ab+2 / b(b+2) > ab+b / b(b+2)
=> A > B
Vậy A > B