
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2.\(P=\frac{x+1}{2x+5}+\frac{x+2}{2x+4}+\frac{x+3}{2x+3}\)
\(=\frac{x+1}{2x+5}+1+\frac{x+2}{2x+4}+1+\frac{x+3}{2x+3}+1-3\)
\(=\frac{3x+6}{2x+5}+\frac{3x+6}{2x+4}+\frac{3x+6}{2x+3}-3\)
\(=\left(3x+6\right)\left(\frac{1}{2x+5}+\frac{1}{2x+4}+\frac{1}{2x+3}\right)-3\)
Áp dụng BĐT Cô-si ta có:
\(a+b+c\ge3\sqrt[3]{abc}\)
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge3\sqrt[3]{\frac{1}{abc}}\)
Nhân vế với vế của 3 BĐT trên ta được:
\(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge3\sqrt[3]{abc}.3\sqrt[3]{\frac{1}{abc}}=9\)
\(\Leftrightarrow\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\frac{9}{a+b+c}\left(1\right)\)
Áp dụng BĐT \(\left(1\right)\)ta được:
\(\frac{1}{2x+5}+\frac{1}{2x+4}+\frac{1}{2x+3}\ge\frac{9}{6x+12}\)
\(\Leftrightarrow\left(3x+6\right)\left(\frac{1}{2x+5}+\frac{1}{2x+4}+\frac{1}{2x+3}\right)-3\ge3\left(x+2\right).\frac{9}{6\left(x+2\right)}-3\)
\(\Leftrightarrow P\ge\frac{3}{2}\left(đpcm\right)\)


b: Để N là số nguyên dương thì \(\sqrt{x}-3>0\)
\(\Leftrightarrow x>9\)
mà x là số nguyên
nên \(\left\{{}\begin{matrix}x\in Z\\x>9\end{matrix}\right.\)

giúp e vs các a cj soyeon_Tiểubàng giải
Phương An
Hoàng Lê Bảo Ngọc
Silver bullet
Nguyễn Huy Tú
Nguyễn Như Nam
Hoàng Tuấn Đăng
Nguyễn Trần Thành Đạt
Nguyễn Huy Thắng
Võ Đông Anh Tuấn


a)\(2^k>2k+1\left(1\right)\)
Với n=3, ta có:\(VT=8;VP=7\), nên (1) đúng nới n=3
Giả sử (1) đúng với \(k=n\), tức là \(2^n>2n+1\left(n\in N\text{*};n\ge3\right)\)
Ta sẽ chứng minh (1) đúng với \(k=n+1\) tức là phải chứng minh \(2^{n+1}>2\left(n+1\right)+1\)
Thật vậy, từ giả thiết quy nạp, ta có:
\(2^{n+1}=2\cdot2^n>2\left(2n+1\right)=4n+2=2n+3+\left(2n-1\right)>2n+3\), do \(\left(n\in N\text{*},n\ge3\right)\)
Vậy (1) đúng với mọi số nguyên \(k\ge3\)
b)\(n^4+6n^3+11n^2+6n\)
\(=n\left(n^3+6n^2+11n+6\right)\)
\(=n\left(n^3+n^2+5n^2+5n+6n+6\right)\)
\(=n\left[\left(n^3+n^2\right)+\left(5n^2+5n\right)+\left(6n+6\right)\right]\)
\(=n\left(n+1\right)\left(n+2\right)\left(n+3\right)\left(n+4\right)⋮120\)
Mà \(120⋮24\) =>Đpcm
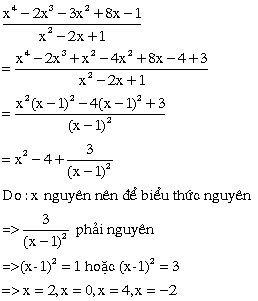
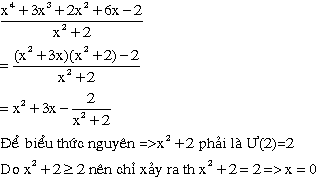 ok bn có thể xem xét mk mk ko chép mạng đâu
ok bn có thể xem xét mk mk ko chép mạng đâu
Đặt A = 52n2−6n+2−12=25n2−3n+1−12≡12n2−3n+1−12(mod13)52n2−6n+2−12=25n2−3n+1−12≡12n2−3n+1−12(mod13)
=>12n2−3n+1−12=12.(12n(n−3)−1)12n2−3n+1−12=12.(12n(n−3)−1)
(12n(n−3)−1)(12n(n−3)−1) chia luôn chia 13 dư 1 do n(n-3) luôn chia hết cho 2
=> 52n2−6n+2−12⋮1352n2−6n+2−12⋮13 mà A lại là số nguyên tố nên A= 13
=> 52n2−6n+2=2552n2−6n+2=25 => n =3
Vậy n = 3
n2−3n+1=n2−n−2n+1n2−3n+1=n2−n−2n+1 là số lẻ nên ta có 52n2−6n+2−12≡1−1n2−3n+1≡0(mod13)52n2−6n+2−12≡1−1n2−3n+1≡0(mod13)
Do đó 52n2−6n+2−12=13⇔52n2−6n+2=25⇔2n2−6n+2=2⇔n=052n2−6n+2−12=13⇔52n2−6n+2=25⇔2n2−6n+2=2⇔n=0 hoặc n=3