KC
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 1 2016
đây là phương trình vô định
2x+5y=13<=>2x=13-5y<=>x=\(\frac{13-5y}{2}=2-2y+\frac{9-y}{2}\)
đặt \(\frac{9-y}{2}=t\)
=>y=9-2t
the vo pt tính t rui tinh x va y
KC
1
19 tháng 2 2016
\(2x+5y=13\Leftrightarrow x=\frac{13-5y}{2}\Rightarrow\)y là số lẻ.
Đặt \(y=2z+1\left(z\in Z\right)\Rightarrow x=4-5z\)
Vậy tập nghiệm nguyên của phương trình là \(\cdot\left(x;y\right)=\left(4-5z;2z+1\right)\)với z nguyên
GK
0
CM
11 tháng 12 2017
Ta có 2 x + 1 3 − y + 1 4 = 4 x − 2 y + 2 5 2 x − 3 4 − y − 4 3 = − 2 x + 2 y − 2
⇔ 40 x + 20 − 15 y − 15 = 48 x − 24 y + 24 6 x − 9 − 4 y + 16 = − 24 x + 24 y − 24
⇔ 8 x − 9 y = − 19 30 x − 28 y = − 31 ⇔ 120 x − 135 = − 285 120 x − 112 = − 124 ⇔ x = 11 2 y = 7
Thay x = 11 2 ; y = 7 vào phương trình 6mx – 5y = 2m – 66 ta được:
6m. 11 2 − 5.7 = 2m – 66 31m = −31 m = −1
Đáp án: A
TN
2
HT
7 tháng 11 2016
Vì (3;5)=1 nên pt có nghiệm nguyên
\(3x-5y=9\\ \Rightarrow y=\frac{3x-9}{5}=\frac{1-2x}{5}+x-2\)
Đặt t=\(\frac{1-2x}{5}\left(t\in Z\right)\)
\(\Rightarrow x=\frac{1-5t}{2}\)\(=\frac{t-1}{2}+1-3t\)
Đặt n=\(\frac{t-1}{2}\left(n\in Z\right)\)\(\Rightarrow t=2n+1\)
\(\Rightarrow\begin{cases}y=t+x-2\\x=n+1-3t\\t=2n+1\end{cases}\Rightarrow\begin{cases}y=-3n-3\\x=-5n-2\end{cases}\left(n\in Z\right)}}\)
N
17 tháng 1 2019
\(\Leftrightarrow y=\dfrac{3x-9}{5}=\dfrac{3\left(x-3\right)}{5}\)\(\Rightarrow x-3⋮5\)\(\Rightarrow x=5k+3\left(k\in Z\right)\)\(\Rightarrow y=\dfrac{3.5k}{5}=3k\)
Vậy pt có vô số nghiệm với nghiệm tổng quát (x;y)=(5k+3\(\left(k\in Z\right)\) ;3k).
To approve a single suggestion, mouse over it and click "✔" Click the bubble to approve all of its suggestions.
CM
14 tháng 4 2018
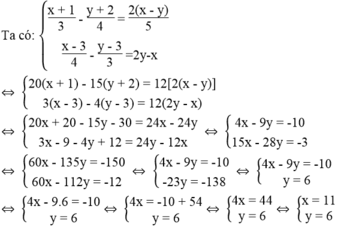
Vì (x; y) = (11; 6) là nghiệm của phương trình 3mx – 5y = 2m +1 nên ta có:
3m.11 – 5.6 = 2m + 1
⇔ 33m – 30 = 2m + 1 ⇔ 31m = 31 ⇔ m = 1
Vậy với m = 1 thì nghiệm của x + 1 3 - y + 2 4 = 2 x - y 5 x - 3 4 - y - 3 3 = 2 y - x cũng là nghiệm của phương trình 3mx – 5y = 2m + 1.
NM
1
6 tháng 11 2019
Có: (2; 5; 1 ) =1
=> Đưa pt trên về dạng: 2x + 5y = 4 +z
Lấy z = u, u thuộc Z
Đặt: c = 4 +u
Ta có phương trình: 2 x + 5 y = c
Phương trình trên có 1 nghiệm riêng là: x0 = 3c và y0 = -c.
=> Phương trình trên có nghiệm tổng quát là: x = 3c + 5t và y = -c -2t với t thuộc Z
Thay c = 4 +u vào ta có nghiệm của pt ban đầu là:
\(\hept{\begin{cases}x=3\left(4+u\right)+5t=12+3u+5t\\y=-\left(4+u\right)-2t=-4-u-2t\\z=u\end{cases}}\)
với u, t bất kì thuộc Z.
x=4
y=1
tick nha
Khánh Cù
x=4
y=1.tick mk di!!!