
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

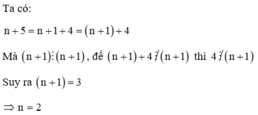

Bài 2:
a: Để E là số nguyên thì \(3n+5⋮n+7\)
\(\Leftrightarrow3n+21-16⋮n+7\)
\(\Leftrightarrow n+7\in\left\{1;-1;2;-2;4;-4;8;-8;16;-16\right\}\)
hay \(n\in\left\{-6;-8;-5;-9;-3;-11;1;-15;9;-23\right\}\)
b: Để F là số nguyên thì \(2n+9⋮n-5\)
\(\Leftrightarrow2n-10+19⋮n-5\)
\(\Leftrightarrow n-5\in\left\{1;-1;19;-19\right\}\)
hay \(n\in\left\{6;4;29;-14\right\}\)

a) \(A=\frac{n-5}{n+1}=\frac{n+1-6}{n+1}=1-\frac{6}{n+1}\)
=> A có giá trị nguyên <=> n + 1 \(\in\){ \(\pm1;\pm2;\pm3;\pm6\)}
| n + 1 | 1 | -1 | 2 | -2 | 3 | -3 | 6 | -6 |
| n | 0 | -2 | 1 | -3 | 2 | -4 | 5 | -7 |
b) Muốn cho \(\frac{n-5}{n+1}\)là phân số tối giản thì (n - 5,n + 1) = 1 . Ta biết rằng nếu (a,b) = 1 thì (a,a - b) = 1 , từ đó suy ra (n - 5,6) = 1
=> (n - 5) không chia hết cho ...(tự điền ra) hay n là số chẵn

a) Để G nguyên thì \(-3⋮\left(n-1\right)\)
\(\Rightarrow\left(n-1\right)\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
Lập bảng:
| \(n-1\) | \(-1\) | \(1\) | \(3\) | \(-3\) |
| \(n\) | \(0\) | \(2\) | \(4\) | \(-2\) |
Vậy \(x\in\left\{-2;0;2;4\right\}\)
b) Để H nguyên thì \(-4⋮\left(2n-1\right)\)
\(\Rightarrow\left(2n-1\right)\inƯ\left(-4\right)=\left\{\pm1;\pm2;\pm4\right\}\)
Mà 2n + 1 là số lẻ nên \(2n-1=\pm1\)
\(TH1:2n-1=-1\)
\(\Leftrightarrow2n=-1+1\)
\(\Leftrightarrow2n=0\)
Mà 2 khác 0 nên n = 0
\(TH1:2n-1=1\)
\(\Leftrightarrow2n=1+1\)
\(\Leftrightarrow2n=2\)
\(\Leftrightarrow n=2\div2\)
\(\Leftrightarrow n=1\)
Vậy n = 0 hoặc n = 1

Tớ nghĩ là cộng vì dấu ''+'' nằm dưới dấu ''='' mà, chắc là quên ấn nút ''Shift'' ấy mà!![]()

1. 3/n-5 thuộc N<=> n-5 lớn hơn 0<=>n lớn hơn 5
2. 3/n-5 thuộc Z<=> n-5 khác 0<=> n khác 5
3. 9/2n-3 thuộc Z<=> 2n-3 khác 0<=> 2n khác 3<=> n thuộc Z

a) - 3 ∉ N
b) 5 ∈ Z
c) 0 ∈ Z
d) 1 ∈ N
e) - 7 ∈ Z
f) 0 ∈ N
g) - 1 ∉ N
h) - 10 ∈ Z

a) \(\left(n+1\right)^2+\left(n+2\right)^2+\left(n+3\right)^2=\left(n+10\right)^2\)
\(\Leftrightarrow n^2+2n+1+n^2+4n+4+n^2+6n+9=n^2+20n+100\)
\(\Leftrightarrow2n^2-8n-86=0\)
\(\Leftrightarrow n^2-4n=43\)
Ta có: \(n^2-4n=n^2-n-3n=n\left(n-1\right)-3n\)
\(n\left(n-1\right)\)là tích hai số tự nhiên liên tiếp nên khi chia cho \(3\)dư \(0\)hoặc \(2\).
Suy ra \(n^2-4n\)chia cho \(3\)dư \(0\)hoặc \(2\).
Mà \(43\)chia cho \(3\)dư \(1\)
do đó phương trình đã cho không có nghiệm tự nhiên.
b) Ta có: \(n^2+h^2+b^2+k^2+n+h+b+k=\left(n^2+n\right)+\left(h^2+h\right)+\left(b^2+b\right)+\left(k^2+k\right)\)
\(=n\left(n+1\right)+h\left(h+1\right)+b\left(b+1\right)+k\left(k+1\right)\)chia hết cho \(2\).
mà \(n+h+b+k\)chia hết cho \(6\)nên chia hết cho \(2\)
suy ra \(n^2+h^2+b^2+k^2\)chia hết cho \(2\)suy ra không phải là số nguyên tố
(do \(n^2+h^2+b^2+k^2>2\)).