Tìm n ∈ N để: a) n + 6 ⋮ n + 2 b) ...

Tìm n ∈ N để:a) n +...

D

Doraemon

20 tháng 2 2018 - olm

Tìm n \(\in\) N để :

a) \(\frac{n+4}{n+2}\in N\)

b) n + 4 \(⋮\)n + 2

c) \(\frac{2n+6}{n+3}\in N\)

d) 2n + 6 \(⋮\)n + 3

#Toán lớp 6

2

U

Uyên

20 tháng 2 2018

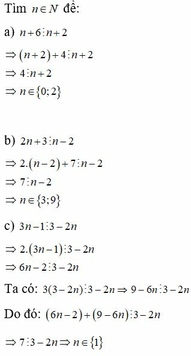
\(b,n+4⋮n+2\)

\(\Rightarrow n+2+2⋮n+2\)

\(n+2⋮n+2\)

\(\Rightarrow2⋮n+2\)

\(\Rightarrow n+2\inƯ\left(2\right)=\left\{1;2\right\}\)

\(\Rightarrow n\in\left\{-1;0\right\}\) mà n thuộc N

=> n = 0

d, \(2n+6⋮n+3\)

\(\Rightarrow2\left(n+3\right)⋮n+3\)

\(n+3⋮n+3\Rightarrow2\left(n+3\right)⋮n+3\)

\(\Rightarrow\) n = bao nhiêu cx đc miễn là n thuộc N

Đúng(0)

TC

Thua Cuộc

20 tháng 2 2018

a)n={-3;-1;-5;0}

b)n={-3;-1;-5;0}

c)n=rỗng

d)n=rỗng

Đúng(0)

KL

Khánh Linh Phạm

25 tháng 10 2016

Bài 1 . Tìm chữ số tận cùng của các lũy thừa :a) 172123b) 243203c) 1791d) 38381e) 81613f) 219423Bài 2 Tìm x ϵ N đểa) 3x + 3x+1 = 36b) 2x + 2x+1 + 2x+2 + 2x+3 = 120c) 5x+ 5x-3= 3150Bài 3 . Tìm n ϵ N đển + 3 và n + 120 đều là số chính...

Đọc tiếp

#Toán lớp 6

1

KL

Khánh Linh Phạm

25 tháng 10 2016

các bạn làm ơn giúp mk với mk đang gấp lắm

Đúng(0)

KK

kaneki ken

25 tháng 7 2017

BT1 : CMR:

a) \(3^{n+3}-3^{n+1}+2^{n+3}+2^{n+2}⋮6\)

b) \(5^n-1⋮4\)

c) \(n^2+n+2⋮5\)

#Toán lớp 6

0

CG

Cô Gái Mộng Mơ

16 tháng 10 2018 - olm

1.tìm x thuộc N)\(\left(x-3\right)^3=2x-6\)2. cho A =\(1+3+3^2+3^3+...+3^n\)a tinh Ab tìm n biết 2A +5 = 313.tìm những điều kiện của n thuộc N để mỗi phép chia sau thực hiện được a \(7^n:7^3\) b\(7^{n+2}:7^6\) c(\(2^{n+1}.5^{n:2}\))...

Đọc tiếp

#Toán lớp 6

0

NK

Nguyễn Kim Ngân

19 tháng 10 2017 - olm

Tìm n \(\in\)N để:

a 6+n \(⋮\)3

b n+3 \(⋮\)n

c n+5 \(⋮\)n+2

Help me now !!!!!

#Toán lớp 6

4

V

Valak

20 tháng 10 2017

a) 6 + n chia hết cho 3

áp dụng tính chất chia hết của 1 tổng

=> n chia hết cho 3

=> n thuộc B(3) = { 0; 3; 6; 9 ; 12 ; .... }

b) Nhắn tin r

c) n + 5 = ( n + 2 ) + 3

=> ( n + 2 ) + 3 chia hết cho ( n + 2 )

áp dụng tính chất chia hết của một tổng

=> 3 chia hết cho n + 2

=> n + 2 thuộc Ư(3) = { 1; 3 }

=> n = { -1 ; 1 }

Đúng(0)

TH

Thắng Hoàng

19 tháng 10 2017

a)nE các {0;3;6;8}

Đúng(0)

LC

Linh Còi

18 tháng 6 2018 - olm

Bài 1: Tìm các số nguyên n để biểu thức sau nhận giá trị nguyên a,\(B=\frac{n}{n-4}\)b,\(C=\frac{2n+7}{n+3}\left(n\ne-3\right)\)c,\(D=\frac{n^3-2n^2+3}{n-2}\)d,\(E=\frac{3n}{n+1}\)e,\(F=\frac{-7}{1-n}\)Bài 2 Cho \(A=\frac{n+1}{\left(n^2+1\right)\left(n-7\right)}\)(n thuộc Z)a, tìm điều kiện của n để A là phân sốb,với n bằng bao nhiêu thì phân số A không tồn tại?c, Tính A, biết n=0,n=1,n=-2Plz làm giúp mình nha <3...

Đọc tiếp

#Toán lớp 6

3

LM

Lê Minh Anh

18 tháng 6 2018

a) Điều kiện xác định: n khác 4

\(B=\frac{n}{n-4}=\frac{n-4+4}{n-4}=\frac{n-4}{n-4}+\frac{4}{n-4}\)\(=1+\frac{4}{n-4}\)

Để B nguyên thì \(\frac{4}{n-4}\in Z\)\(\Rightarrow n-4\in U\left(4\right)=\left(1;-1;2;-2;4;-4\right)\)

\(\Rightarrow n\in\left\{5;3;6;2;8;0\right\}\)(thỏa mãn n khác 4)

Vậy .............

b) \(n\in\left\{-2;-4\right\}\)

c) \(n\in\left\{-2;-1;3;5\right\}\)

d) \(n\in\left\{0;-2;2;-4\right\}\)

e) \(n\in\left\{0;2;-6;8\right\}\)

(Bài này có 1 bạn hỏi rồi bạn nhé!!!)

Bài 2: a) Để A là phân số thì (n² +1)(n-7) khác 0 <=> n khác 7

b) Với n = 7 thì mẫu số bằng 0 => phân số không tồn tại

c) Với n = 0 thì \(\frac{0+1}{\left(0^2+1\right)\left(0-7\right)}=\frac{1}{-7}\left(=\frac{-1}{7}\right)\)

Với n = 1 thì \(\frac{1+1}{\left(1^2+1\right)\left(1-7\right)}=\frac{2}{2\times\left(-6\right)}=\frac{-1}{6}\)

Với n = -2 thì: \(\frac{-2+1}{\left[\left(-2\right)^2+1\right]\left(-2-7\right)}=\frac{-1}{-45}=\frac{1}{45}\)

Đúng(0)

KN

Khánh Ngọc

13 tháng 7 2020

Ta có :

\(B=\frac{n}{n-4}=\frac{n-4+4}{n-4}=1+\frac{4}{n-4}\)

Để \(B\in Z\) thì \(\frac{4}{n-4}\in Z\)

\(\Rightarrow n-4\in\left\{\pm1;\pm2;\pm4\right\}\)

\(\Rightarrow n\in\left\{0;2;3;5;6;8\right\}\)

Đúng(0)

LD

Lê Duy Hiếu

3 tháng 3 2020 - olm

Tìm n\(\in\)N để:

a) n + 2 \(⋮\)n - 1

b) 2n + 7\(⋮\)n + 1

c) 2n + 1\(⋮\)6 - n

d) 4n + 3\(⋮\)2n + 6

#Toán lớp 6

4

H2

•๖ۣۜHυүềη ²ƙ⁷ ( ๖ۣۜTεαм ๖ۣۜBạ¢ɦ ๖ۣۜ...

3 tháng 3 2020

a) => n-1+3 chia hết n-1

Mà n-1 chia hết n-1

=> 3 chia hết cho n-1

=> n-1 thuộc Ước của 3

........

b)=> 2(n+1) +5 chia hết n+1

mà 2(n+1) chia hết n+1

=> 5 chia hết cho n+1

=> n+1 thuộc ước của 5

.......

Đúng(0)

NF

Napkin ( Fire Smoke Team )

3 tháng 3 2020

a,Ta có :\(n+2⋮n-1\)

\(=>n-1+3⋮n-1\)

Do \(n-1⋮n-1\)

\(=>3⋮n-1\)

\(=>n-1\inƯ\left(3\right)\)

\(=>n-1\in\left\{-3;-1;1;3\right\}\)

\(=>n\in\left\{-2;0;2;4\right\}\)

b,\(2n+7⋮n+1\)

\(=>2.\left(n+1\right)+5⋮n+1\)

Do \(2.\left(n+1\right)⋮n+1\)

\(=>5⋮n+1\)

\(=>n+1\inƯ\left(5\right)\)

\(=>n+1\in\left\{-5;-1;1;5\right\}\)

\(=>n\in\left\{-6;-2;0;4\right\}\)

Đúng(0)

DD

Dương Đình Hưởng

4 tháng 12 2017 - olm

Chứng minh:

a) 1+ 2+ 3+ ...+( n- 1)+ n= \(\frac{n\left(n+1\right)}{2}\).

b) 1\(^2\)+ 2\(^2\)+ 3\(^2\)+...+( n- 1)\(^2\)+ n\(^2\)= \(\frac{n\left(n+1\right)\left(2n+1\right)}{6}\).

c) 1\(^3\)+ 2\(^3\)+ 3\(^3\)+...+( n- 1)\(^3\)+ n\(^3\)= \(\left[\frac{n\left(n+1\right)}{2}\right]^2\).

#Toán lớp 6

1

MN

mi ni on s

4 tháng 12 2017

mk năm nay học lớp 8 mà mới chỉ học công thức thôi chứ chưa học (hoặc đã học mà quên mất) nhưng chứng minh cái này mk mới chỉ học công thức thôi chứ chứng minh bài toán tổng quánthì chịu

Đúng(0)

TD

Tiến Dũng

18 tháng 1 2017 - olm

Tìm n\(\in\)Z để:

a) 6\(⋮\)(n-2)

b) ( n+2 ) \(⋮\)( n-3 )

#Toán lớp 6

2

VN

Vũ Như Mai

18 tháng 1 2017

a) n - 2 \(\in\)Ư(6) = {-1;1;2;-2;3;-3;6;-6}

Sau đó b thay số vào n - 2 = .. để tìm n nha :)

b) (n + 2) \(⋮\)(n - 3)

=> (n-3+5) \(⋮\)(n-3)

Mà (n-3) \(⋮\)(n-3)

=> (n-3) \(\in\)Ư(5) = {-1;1;5;-5}

Rồi cũng thay số như câu a

Đúng(0)

TV

Trần Việt Anh

18 tháng 1 2017

=>n-2 thuộc Ư(6)={1;-1;2;-2;3;-3;6;-6}

rồi lập bản thử từng TH nhé

Đúng(0)

LD

Lê Duy Hiếu

3 tháng 3 2020 - olm

Tìm n\(\in\)N để:

a) n + 5 \(⋮\)n + 2

b) 2n + 3\(⋮\)n - 2

c) 3n + 1\(⋮\)11 - 2n

d) n² + 4\(⋮\)n + 1

#Toán lớp 6

2

IA

I am➻Minh

3 tháng 3 2020

\(a,\frac{n+5}{n+2}=\frac{n+2+3}{n+2}=1+\frac{3}{n+2}\)

Để \(n+5⋮n+2\) thì \(n+2\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)

Xét bảng ( tự xét nha )

KL..

\(b,\frac{2n+3}{n-2}=\frac{2\left(n-2\right)+7}{n-2}=2+\frac{7}{n-2}\)

Giải các ý khác tương tự như trên

Đúng(0)

TL

Tran Le Khanh Linh

3 tháng 3 2020

Ta có n+5=n+2+3

Để n+5 chia hết cho n+2 thì n+2+3 chia hết cho n+2

Mà n thuộc n => n+2 thuộc N

=> n+2 thuộc Ư (5)={1;5}
Nếu n+2=1 => n=-1 (ktm)

Nếu n+1=5 => n=4(tm)

Vậy n=4 thì n+5 chia hết cho n+2

b) Ta có 2n+3=2(n-2)+7

Để 2n+3 chia hết cho n-2 thì 2(n-2)+7 chia hết cho n-1

n thuộc N => n-1 thuộc N

=> n-1 thuộc Ư (7)={1;7}

Nếu n-1=1 => n=2(tm)

Nếu n-1=7 => n=8 (tm)

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP