
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{n+8}{7}\)có giá trị nguyên
th1 \(\frac{n+8}{7}\) là nguyên dương
\(\Leftrightarrow\orbr{\begin{cases}n+8>0\\7>0\end{cases}\Leftrightarrow\orbr{\begin{cases}n>-8\\7>0\end{cases}\Leftrightarrow}-8< n< 0< 7}\)
\(\Leftrightarrow\orbr{\begin{cases}n+8< 0\\7< 0\end{cases}\Leftrightarrow\orbr{\begin{cases}n< -8\\7< 0\end{cases}\Leftrightarrow}-8>n>0>7\left(l\right)}\)
th2\(\frac{n+8}{7}\)là nguyên âm
\(\Leftrightarrow\orbr{\begin{cases}n+8>0\\7< 0\end{cases}\Leftrightarrow\orbr{\begin{cases}n>-8\\7< 0\end{cases}\Leftrightarrow}-8< n< 7< 0\left(l\right)}\)
\(\Leftrightarrow\orbr{\begin{cases}n+8< 0\\7>0\end{cases}\Leftrightarrow\orbr{\begin{cases}n< -8\\7>0\end{cases}\Leftrightarrow}-8>n>7>0\left(l\right)}\)
th3 \(\frac{n+8}{7}=0\)
\(\Leftrightarrow\orbr{\begin{cases}n+8=0\\7=0\left(l\right)\end{cases}}\Leftrightarrow n=-8\)
cộng các th ta có
\(-8\le n< 0< 7\)
vậy với\(-8\le n< 0< 7\)thì phân số có giá trị nguyên


Để phân số :\(\frac{2n+3}{7}\) có giá trị là số nguyên thì 2n+3:7
\(\implies\) \(2n+3=7k\)
\(\implies\) 2n=7k-3
\(\implies\) n=\(\frac{7k-3}{2}\)
Vậy với mọi số nguyên n có dang \(\frac{7k-3}{2}\) thì phân số \(\frac{2n+3}{7}\) có giá trị là số nguyên

\(\frac{2n+3}{n+2}=\frac{2n+4-1}{n+2}=2-\frac{1}{n+2}\inℤ\)
mà \(n\inℤ\Rightarrow n+2\inƯ\left(1\right)=\left\{-1;1\right\}\Leftrightarrow n\in\left\{-3;-1\right\}\).


c) Để \(\dfrac{2n+5}{n-3}\) ∈ Z thì 2n+5⋮n-3
⇒ 2n-3+8⋮n-3
⇒ 8⋮n-3 ⇒ n-3∈Ư(8)
Ư(8)={...}
⇒n=...
;-------------------------------; làm hết đeeeeeeeeeeeeeeeeeeeeeeeeeeeee

a, để B là số nguyên thì 6n+7 chia hết cho 2n+3
=> 6n+9-2 chia hết cho 2n+3
Vì 6n+9 chia hết cho 2n+3
=> 2 chia hết cho 2n+3
Mà 2n+3 lẻ
=> 2n+3 thuộc ước lẻ của 2
| 2n+3 | n |
| 1 | -1 |
| -1 | -2 |
KL: n\(\in\){-1; -2}


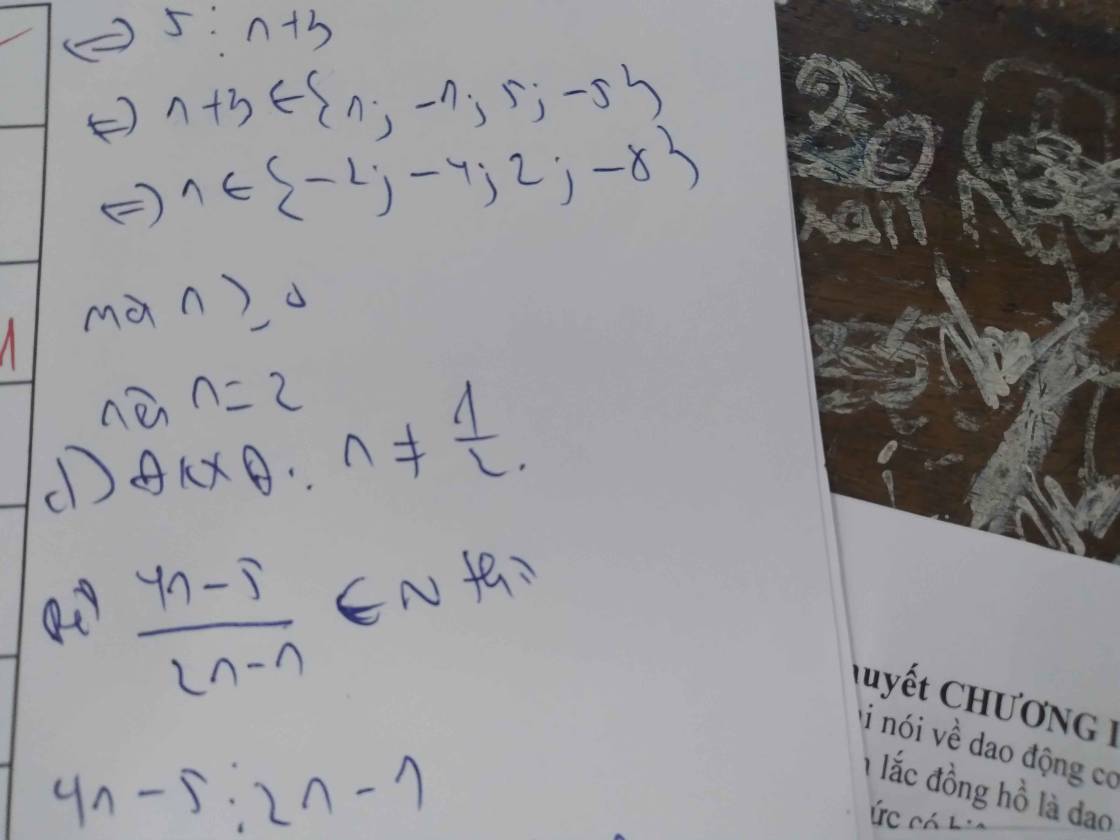

riêng từng phân số hay cả 2 phân số đều là số nguyên vậy bạn!