Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhân tử với 2, gửi nguyên mẫu=> Phân số đấy gấp hai lần phân số cũ=> Bằng 2 lần hiệu hai phần số đó
Phân số mới là: 7/36x2=7/18
=>7/18
Theo mk nghi thui nha:
Gọi phân số ban đầu là a/b (b>0)
Thì phân số mới sẽ là 2a/b ( vì ta nhân tử số với 2 và giữ nguyên mẫu số)
Theo đầu bài ta có: 2a/b-a/b=7/36
(2a-a)/b=7/36
a/b=7/36
Vậy phân số cần tìm là 7/36

1.
1 người làm xong công việc trong:
12 x 5 = 60 ( ngày )
Muốn làm xong công việc trong 4 ngày thì cần số người là:
60 : 4 = 15 ( người )
Đáp số: 15 người
2.thiếu đề
4.
Số nhỏ nhất có 7 chữ số khác nhau chia hết cho 9 : 1023489
HT~

Gợi ý: Khi ta nhân 1 phân số với số tự nhiên, ta chỉ việc nhân tử số của phân số với số tự nhiên đó và giữ nguyên mẫu số. Vậy nhân tử số của phân số với 2 , giữ nguyên mẫu số tức là ta gấp phân số đó lên 2 lần. Bài toán được chuyển về dạng: tìm 2 số biết hiệu và tỉ số.
Giải
Nếu nhân tử số của phân số với 2 và giữ nguyên mẫu số thì ta được phân số mới gấp 2 lần phân số ban đầu. Ta có sơ đồ sau:
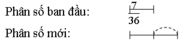
Phân số ban đầu là: 7/36: (2 - 1) = 7/36
Thử lại: 7 x 2 36 - 7 36 = 7 36

Gọi phân số đó là \(\frac{a}{b}\)
Ta có: \(\frac{a}{b}=\frac{9}{10}\)
Theo bài cho: \(\frac{a-15}{b}=\frac{3}{4}\) => \(\frac{a}{b}-\frac{15}{b}=\frac{3}{4}\). Thay \(\frac{a}{b}=\frac{9}{10}\) ta được
\(\frac{9}{10}-\frac{15}{b}=\frac{3}{4}\)=> \(\frac{15}{b}=\frac{9}{10}-\frac{3}{4}=\frac{3}{20}\Rightarrow\frac{15}{b}=\frac{15}{100}\)
=> b = 100 => \(\frac{a}{100}=\frac{9}{10}=\frac{90}{100}\) => a = 90
Vậy phân số đã cho là 90/100

Nếu thêm 4 vào tử và giữ nguyên mẫu thì được phân số mới có giá trị bằng 1. Vậy => Mẫu số hơn tử số 4 đơn vị.
- Nếu thêm 9 vào mẫu và giữ nguyên tử số thì khi đó mẫu số hơn tử số :
4 + 9 = 13 (đơn vị)
- Tử số ban đầu là :
13 : (2 - 1) x 1 = 13
- Mẫu số ban đầu là :
13 + 4 = 17
Vậy phân số phải tìm là 13171317
k cho mìn nhé

Lời giải:
Nếu lấy mẫu của phân số đó chia cho 4 và giữ nguyên tử số thì được phân số mới gấp 4 lần phân số ban đầu
Tỉ số: 4
Hiệu: $\frac{9}{8}$
Phân số ban đầu là: $\frac{9}{8}: (4-1)\times 1=\frac{3}{8}$
\(\dfrac{9}{32}\)