Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Tọa độ đỉnh của (P) là:
\(\begin{cases}x=-\frac{b}{2a}=\frac{4m}{2\cdot2}=\frac{4m}{4}=m\\ y=-\frac{b^2-4ac}{4a}=-\frac{\left(-4m\right)^2-4\cdot2\cdot5}{4\cdot2}=-\frac{16m^2-40}{8}=-2m^2+5\end{cases}\)
Ta có: \(y=-2m^2+5\le5\forall m\)
Dấu '=' xảy ra khi m=0
b: Phương trình hoành độ giao điểm là:
\(2x^2-4mx+5=5\)
=>\(2x^2-4mx=0\)
=>\(x^2-2mx=0\)
=>x(x-2m)=0
=>\(\left[\begin{array}{l}x=0\\ x=2m\end{array}\right.\)
Để A và B là hai điểm phân biệt thì 2m<>0
=>m<>0
A(0;5); B(2m;5)
\(AB=\sqrt6\)
=>\(AB^2=6\)
=>\(\left(2m-0\right)^2+\left(5-5\right)^2=6\)
=>\(4m^2=6\)
=>\(m^2=\frac64\)
=>\(\left[\begin{array}{l}m=\frac{\sqrt6}{2}\left(nhận\right)\\ m=-\frac{\sqrt6}{2}\left(nhận\right)\end{array}\right.\)

2. \(|x| +|x-1| ≤ 5 \\ \Leftrightarrow |x| + |x-1| ≤ \dfrac{5}{2}\)
| \(-∞\) | \(0\) | \(1\) | \(+∞\) | |
| \(|x|\) | \(-x\) | \(x\) | \(x\) | \(x\) |
| \(|x-1|\) | \(1-x\) | \(1-x\) | \(x-1\) | \(x-1\) |
| \(|x|+|x-1|\) | \(1-2x\) | \(1\) | \(2x-1\) | \(2x-1\) |
TH1: \(1-2x ≤ \dfrac{5}{2} \Leftrightarrow x ≥ \dfrac{-3}{4}\)
TH2: \(2x-1 ≤ \dfrac{5}{2} \Leftrightarrow x ≤ \dfrac{7}{4}\)
Vậy....

b, \(\left\{{}\begin{matrix}x^2-2x-3\le0\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1\le x\le3\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
Yêu cầu bài toán thỏa mãn khi phương trình \(f\left(x\right)=x^2-2mx+m^2-9\ge0\) có nghiệm \(x\in\left[-1;3\right]\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2-m^2+9=9>0,\forall m\\-1< m< 3\\f\left(-1\right)=m^2+2m-8\ge0\\f\left(3\right)=m^2-6m\ge0\end{matrix}\right.\)
\(\Leftrightarrow m\in[2;3)\cup(-1;0]\)


Tham khảo:
Đỉnh S có tọa độ: \({x_S} = \dfrac{{ - b}}{{2a}} = \dfrac{{ - 2}}{{2.1}} = - 1;\,{y_S} = {\left( { - 1} \right)^2} + 2.( - 1) + 3 = 2.\)
Hay \(S\left( { - 1;2} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:
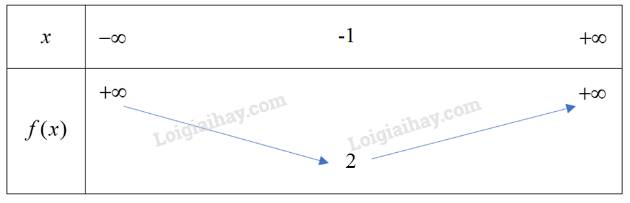
Hàm số đạt giá trị nhỏ nhất bằng \(2\).

Lời giải:
$x^2-2x-3=x(x+3)-5(x+3)+12=(x+3)(x-5)+12$
Vì $x\in [-3;4]$ nên $x+3\geq 0; x-5< 0$
$\Rightarrow x^2-2x-3=(x+3)(x-5)+12\leq 12$
Vậy GTLN của hàm số là $12$ khi $x=-3$