Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ukm
It's very hard
l can't do it
Sorry!

Câu 1: Sửa lạ đề chút nhé : 4x + 1 -> 4x -1
Đặt A = \(\sqrt{2x+\sqrt{4x-1}}+\sqrt{2x-\sqrt{4x-1}}\)
=> \(\sqrt{2}.A\)= \(\sqrt{4x-1+2\sqrt{4x-1}+1}+\sqrt{4x-1-2\sqrt{4x-1}+1}\)
= \(\sqrt{\left(\sqrt{4x-1}+1\right)^2}+\sqrt{\left(\sqrt{4x-1}-1\right)^2}\)
= \(\left|\sqrt{4x-1}+1\right|+\left|\sqrt{4x-1}-1\right|\)
Vì \(\frac{1}{4}< x< \frac{1}{2}\Rightarrow0< 4x-1< 1\Rightarrow0< \sqrt{4x-1}< 1\)
nên \(\sqrt{2}A=\)\(\sqrt{4x-1}+1+1-\sqrt{4x-1}\)=2
=> \(A=2:\sqrt{2}=\sqrt{2}\)
Câu 2. Có: \(9-4\sqrt{2}=8-2.2\sqrt{2}+1=\left(2\sqrt{2}-1\right)^2\)
=> \(\sqrt{9-4\sqrt{2}}=2\sqrt{2}-1\)
=> \(4+\sqrt{9-4\sqrt{2}}=4+2\sqrt{2}-1=2+2\sqrt{2}+1=\left(\sqrt{2}+1\right)^2\)
=> \(\sqrt{4+\sqrt{9-4\sqrt{2}}}=\sqrt{2}+1\)
=> \(53-20\sqrt{4+\sqrt{9-4\sqrt{2}}}=53-20\left(\sqrt{2}+1\right)=33-2.10\sqrt{2}=5^2-2.5.2\sqrt{2}+8=\left(5-2\sqrt{2}\right)^2\)
=> \(\sqrt{53-20\sqrt{4+\sqrt{9-4\sqrt{2}}}}=5-2\sqrt{2}\)
\(\sqrt{2x+\sqrt{4x-1}}+\sqrt{2x-\sqrt{4x-1}}\)

a/\(\sqrt{x}=7\)
\(\Leftrightarrow x=49\)
b/\(\Leftrightarrow x< 4\)(do x>0)
\(\Rightarrow x\varepsilon\left\{0;1;2;3\right\}\)
c/\(2x< 16\)
\(\Leftrightarrow x< 8\)
\(\Leftrightarrow x\varepsilon\left\{1;2;3;4;5;6;7\right\}\)
a) \(2\sqrt{x}=14\Leftrightarrow\sqrt{x}=7\)
\(\Leftrightarrow x=7^2\Leftrightarrow x=49\)
b) \(\sqrt{x}< \sqrt{2}\Leftrightarrow x< 2\)
c) \(\sqrt{2x}< 4\)
Vì \(4=\sqrt{16}\text{ nên }\sqrt{2x}< 4\text{ có nghĩa là }\sqrt{2x}< 16\)
\(\Leftrightarrow2x< 16\)
\(\Leftrightarrow x< 8\left(x\ge0\right)\)

a, \(\sqrt{4-2\sqrt{3}}-\sqrt{3}=\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{3}=\sqrt{3}-1-\sqrt{3}=-1\)
b,\(\sqrt{11+6\sqrt{2}}-3+\sqrt{2}=\sqrt{\left(\sqrt{2}+3\right)^2}-3+\sqrt{2}=\sqrt{2}+3-3+\sqrt{2}=2\sqrt{2}\)
c, \(\sqrt{9x^2}-2x=\sqrt{\left(3x\right)^2}-2x=3x-2x=x\)
d, câu này sai đề rồi , nếu sửa lại phải như này :
\(x-4+\sqrt{16-8x+x^2}=x-4+\sqrt{\left(4-x\right)^2}=x-4+4-x=0\)
a) \(\sqrt{4-2\sqrt{3}}-\sqrt{3}=\sqrt{\left(\sqrt{3}-1\right)^2}-\sqrt{3}\)=\(\sqrt{3}-1-\sqrt{3}=-1\)
b) \(\sqrt{11+6\sqrt{2}}-3+\sqrt{2}\) = \(\sqrt{\left(3+\sqrt{2}\right)^2}-3+\sqrt{2}\)
= \(3+\sqrt{2}-3+\sqrt{2}\) = \(2\sqrt{2}\)
c) \(\sqrt{9x^2}-2x=\sqrt{\left(3x\right)^2}-2x\) = \(\left|3x\right|-2x=-3x-2x\) (x < 0)
= \(-5x\)
d) \(x-4+\sqrt{16-8x+x^2}\) \(\left(x>4\right)\) = \(x-4+\sqrt{\left(4-x\right)^2}\)
= \(x-4+\left|4-x\right|\) = \(x-4-4+x\) ( \(x>4\))
= \(2x-8\)

Với câu c, Thiên Anh nên thêm điều kiện để phần kết luận là: \(0\le x< 2.\)

a) 1
b) \(2\sqrt{x-2}+\sqrt{x+2}\)
c)câu này để bạn tự làm nhé
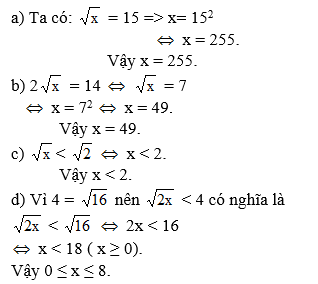
\(A=2x+\sqrt{4-2x^2}=\sqrt{2}.\sqrt{2x^2}+\sqrt{4-2x^2}\)
áp dụng BĐT bunhiacopxki,ta có:
\(A^2\le\left(2+1\right)\left(2x^2+4-2x^2\right)=3.4=12\)
\(\Leftrightarrow A\le\sqrt{12}\)
dấu = xảy ra khi \(\frac{\sqrt{2}}{\sqrt{2}x}=\frac{1}{\sqrt{4-2x^2}}\Leftrightarrow4-2x^2=x^2\Leftrightarrow x=\sqrt{\frac{4}{3}}=\frac{2}{\sqrt{3}}\)
vậy Amax = \(\sqrt{12}\)khi x=\(\frac{2}{\sqrt{3}}\)