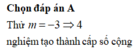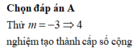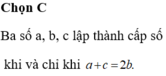Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(C) giao Ox tại 3 điểm <=> x^3-(2m+1)x^2-9x=0 có 3nghiệm pbiệt
<=> x( x^2- ( 2m+1)x-9)=0 có 3 nghiệm pbiệt
<=> x=0
x^2- ( 2m+1)x-9=0 (*)có 2 nghiệm pbiệt <=> denta >0
gọi x1, x2 là 2 nghiệm của (*)
3 nghiệm của đề là x1;0 ; x2
ta có x1+x2=0 dùng viet
phuong trinh hoanh do giao diem la: x3-(2m+1)x2-9x=0. <=> x[x2 -(2m+1)x-9] =0 ta giai dc x=o va x2-(2m+1)x-9=0 ta dat g(x)=x2-(2m+1)x-9 de cm cat truc hoanh tai 3 diem pb thi g(x)=o phai co 2 nghiem pb khac 0. <=>Δ>0 =>m goi x1, x2 la nghiem cua g(x) de lap thanh cap so cong thi x2=9x1 Ap dung vi-et tim ra la dc![]()

Phương trình hoành độ giao điểm : \(-x^4+2\left(2+m\right)x^2-3-2m=0\left(1\right)\)
Đặt \(t=x^2,\left(t\ge0\right)\), phương trình (1) trở thành : \(t^2-1\left(m+2\right)t+3+2m=0\left(2\right)\)
(1) có 4 nghiệm phân biệt khi và chỉ khi (2) có 2 nghiệm dương phân biệt
Điều kiện là : \(\begin{cases}\Delta'>0\\S>0\\P>0\end{cases}\) \(\Leftrightarrow\begin{cases}m^2+2m+1>0\\m+2>0\\3+2>0\end{cases}\) \(\Leftrightarrow\begin{cases}m\ne-1\\m>-\frac{3}{2}\end{cases}\) (*)
Với điều kiện (*), giả sử \(t_1;t_2\) (\(0 < t 1 < t2 \) là 2 nghiệm phân biệt của (2), khi đó (1) có 4 nghiệm phân biệt là \(x_1=-\sqrt{t_2};x_2=-\sqrt{t_1};x_3=\sqrt{t_1};x_4=\sqrt{t_2};\)
\(x_1;x_2;x_3;x_4\) lập thành một cấp số cộng khi và chỉ khi :
\(x_2-x_1=x_3-x_2=x_4-x_3\)
\(\Leftrightarrow t_2=9t_1\left(a\right)\)
Áp dụng định lí Viet ta có : \(t_1+t_2=2\left(m+2\right);t_1.t_2=3+2m\left(b\right)\)
Từ (a) và (b) ta có : \(9m^2-14m-39=0\)
Đối chiếu điều kiện (*) ta có \(m=3\) hoặc \(m=-\frac{13}{9}\)