
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TD
1

Các câu hỏi dưới đây có thể giống với câu hỏi trên
MQ
0

PT
1

CM
4 tháng 1 2018
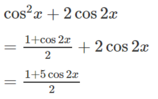
Vì -1 ≤ cos2x ≤ 1 nên giá trị lớn nhất của y là 3, đạt được khi x = 0, giá trị nhỏ nhất của y là -2, đạt được khi x = π/2

NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 9 2021
1. Không dịch được đề
2.
\(-1\le cos2x\le1\Rightarrow1\le y\le3\)
3.
a. \(-2\le2sinx\le2\Rightarrow-1\le y\le3\)
\(y_{min}=-1\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)
\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
b.
\(0\le cos^2x\le1\Rightarrow-1\le y\le2\)
\(y_{min}=-1\) khi \(cos^2x=1\Rightarrow x=k\pi\)
\(y_{max}=2\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
4.
\(y=\left(tanx-1\right)^2+2\ge2\)
\(y_{min}=2\) khi \(tanx=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)
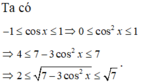
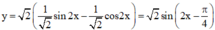
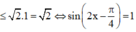
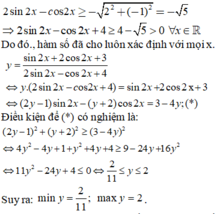
\(y.cos2x+2y=cos2x+m.sin2x+1\)
\(\Leftrightarrow m.sin2x+\left(1-y\right)cos2x=2y-1\)
\(\Rightarrow m^2+\left(1-y\right)^2\ge\left(2y-1\right)^2\)
\(\Rightarrow3y^2-2y-m^2\le0\)
\(\Rightarrow\dfrac{1-\sqrt{1+3m^2}}{3}\le y\le\dfrac{1+\sqrt{1+3m^2}}{3}\)
Bạn coi lại đề, m càng lớn thì max y càng lớn. Câu hỏi chính xác của đề bài là gì?