CN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 3 2021
Với \(m=2\Rightarrow6x^2+3=0\) (vô nghiệm)
Với \(m\ne2\) đặt \(x^2=t\ge0\Rightarrow\left(m-2\right)t^2-2\left(m+1\right)t-3=0\) (1)
Ứng với mỗi \(t>0\Rightarrow\) luôn có 2 giá trị x phân biệt tương ứng thỏa mãn
\(\Rightarrow\) Pt đã cho có đúng 2 nghiệm pb khi và chỉ khi (1) có 2 nghiệm trái dấu
\(\Leftrightarrow ac< 0\Leftrightarrow-3\left(m-2\right)< 0\Leftrightarrow m>2\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 12 2020
ĐKXĐ: \(x\ge0\)
\(\left(x^2-x-m\right)\sqrt{x}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-x-m=0\left(1\right)\end{matrix}\right.\)
Giả sử (1) có nghiệm thì theo Viet ta có \(x_1+x_2=1>0\Rightarrow\left(1\right)\) luôn có ít nhất 1 nghiệm dương nếu có nghiệm
Do đó:
a. Để pt có 1 nghiệm \(\Leftrightarrow\left(1\right)\) vô nghiệm
\(\Leftrightarrow\Delta=1+4m< 0\Leftrightarrow m< -\dfrac{1}{4}\)
b. Để pt có 2 nghiệm pb
TH1: (1) có 1 nghiệm dương và 1 nghiệm bằng 0
\(\Leftrightarrow m=0\)
TH2: (1) có 2 nghiệm trái dấu
\(\Leftrightarrow x_1x_2=-m< 0\Leftrightarrow m>0\)
\(\Rightarrow m\ge0\)
c. Để pt có 3 nghiệm pb \(\Leftrightarrow\) (1) có 2 nghiệm dương pb
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=1+4m>0\\x_1x_2=-m>0\\\end{matrix}\right.\) \(\Leftrightarrow-\dfrac{1}{4}< m< 0\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 11 2021
\(\Leftrightarrow\left(x^2-2x+5\right)\left(x^2-2x-3\right)=m\)
Đặt \(x^2-2x-3=t\) (1)
(1) có 2 nghiệm x phân biệt khi \(\Delta'=1-\left(-3-t\right)>0\Rightarrow t>-4\)
Khi đó pt đã cho trở thành:
\(\left(t+8\right)t=m\)
\(\Leftrightarrow t^2+8t=m\) (2)
Do (2) là pt bậc 2 có tối đa 2 nghiệm nên pt đã cho có 4 nghiệm pb khi và chỉ khi (2) có 2 nghiệm pb đều lớn hơn -4
Từ đồ thị \(f\left(t\right)=t^2+8t\) ta thấy ko tồn tại m thỏa mãn
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 9 2021
\(x^3-x^2+2mx-2m=0\)
\(\Leftrightarrow x^2\left(x-1\right)+2m\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+2m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x^2=-2m\end{matrix}\right.\)
Để pt có 3 nghiệm \(\Rightarrow-2m>0\Rightarrow m< 0\)
a. Do vai trò 3 nghiệm như nhau, ko mất tính tổng quát giả sử \(x_1=1\) và \(x_2;x_3\) là nghiệm của \(x^2+2m=0\)
Để pt có 3 nghiệm pb \(\Rightarrow\left\{{}\begin{matrix}-2m>0\\-2m\ne1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< 0\\m\ne-\dfrac{1}{2}\end{matrix}\right.\)
Khi đó: \(x_2+x_3=0\Rightarrow x_1+x_2+x_3=1\ne10\) với mọi m
\(\Rightarrow\) Không tồn tại m thỏa mãn yêu cầu
b.
Giả sử pt có 3 nghiệm, khi đó \(\left[{}\begin{matrix}x_2=-\sqrt{-2m}< 0< 1\\x_3=\sqrt{-2m}\end{matrix}\right.\)
\(\Rightarrow\) Luôn có 1 nghiệm của pt âm \(\Rightarrow\) không tồn tại m thỏa mãn
Em coi lại đề bài
HP
16 tháng 2 2021
a, Phương trình có hai nghiệm trái dấu khi \(2\left(2m^2-3m-5\right)< 0\)
\(\Leftrightarrow\left(2m-5\right)\left(m+1\right)< 0\)
\(\Leftrightarrow-1< m< \dfrac{5}{2}\)
b, TH1: \(m^2-3m+2=0\Leftrightarrow\left[{}\begin{matrix}m=1\\m=2\end{matrix}\right.\)
Phương trình đã cho có nghiệm duy nhất
TH2: \(m^2-3m+2\ne0\Leftrightarrow\left\{{}\begin{matrix}m\ne1\\m\ne2\end{matrix}\right.\)
Phương trình có hai nghiệm trái dấu khi \(-5\left(m^2-3m+2\right)< 0\)
\(\Leftrightarrow m^2-3m+2>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>2\\m< 1\end{matrix}\right.\)
Vậy \(m>2\) hoặc \(m< 1\)
29 tháng 12 2020
Đặt x2 + 2x + 4 = t . Điều kiện : t ≥ 3
Phương trình đã cho trở thành t2 - 2mt - 1 = 0 (1)
(1) là phương trình hoành độ giao điểm của đồ thị hàm số y = t2 - 2mt - 1 với trục Ox (tức đường thẳng y = 0). Yêu cầu bài toán thỏa mãn khi (1) có 2 nghiệm phân biệt t thỏa mãn t ≥ 3
Ta có bảng biến thiên của hàm số y = t2 - 2mt - 1
Nếu m > 3 thì yêu cầu bài toán thỏa mãn khi
8 - 6m ≥ 0 ⇔ m ≤ \(\dfrac{4}{3}\) (không thỏa mãn m > 3)
Nếu m < 3, yêu cầu bài toán thỏa mãn khi
8 - 6t ≤ 0 ⇔ m ≥ \(\dfrac{4}{3}\) Vậy m ∈ \(\)[\(\dfrac{4}{3};3\))
Nếu m = 3 thì phương trình trở thành
t2 - 6t - 1 = 0 có 2 nghiệm thỏa mãn \(\left\{{}\begin{matrix}t_1+t_2=6\\t_1.t_2=-1\end{matrix}\right.\)
tức phương trình có 2 nghiệm trái dấu (không thỏa mãn điều kiện 2 nghiệm t ≥ 3) nên m = 3 không thỏa mãn yêu cầu bài toán
Vậy tập hợp các giá trị m thỏa mãn yêu cầu bài toán là M = \(\left\{m\in R;\dfrac{4}{3}\le m< 3\right\}\)
HP
5 tháng 1 2021
1.
Yêu cầu bài toán thỏa mãn khi:
\(\left\{{}\begin{matrix}\Delta=25-12m>0\\x_1^2+x_2^2< 17\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{25}{12}\\\left(x_1+x_2\right)^2-2x_1x_2< 17\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{25}{12}\\\left(2m-3\right)^2-2\left(m^2-4\right)< 17\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< \dfrac{25}{12}\\2m^2-12m< 0\end{matrix}\right.\)
\(\Leftrightarrow0< m< \dfrac{25}{12}\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 7 2021
Với \(x=0\) ko phải nghiệm
Với \(x\ne0\) chia 2 vế cho \(x^2\) ta được:
\(x^2+\dfrac{1}{x^2}+3x+\dfrac{3}{x}+m=0\)
\(\Leftrightarrow\left(x+\dfrac{1}{x}\right)^2+3\left(x+\dfrac{1}{x}\right)+m-2=0\) (1)
Đặt \(x+\dfrac{1}{x}=t\Rightarrow x^2-tx+1=0\) (2)
(2) có 2 nghiệm pb khi và chỉ khi:
\(\Delta=t^2-4>0\Rightarrow\left[{}\begin{matrix}t>2\\t< -2\end{matrix}\right.\)
Khi đó (1) trở thành:
\(t^2+3t+m-2=0\) (3)
Pt đã cho có 4 nghiệm pb khi và chỉ khi (3) có 2 nghiệm pb thỏa mãn \(\left[{}\begin{matrix}t>2\\t< -2\end{matrix}\right.\)
(3) \(\Leftrightarrow t^2+3t-2=-m\)
Đặt \(f\left(t\right)=t^2+3t-2\)
\(f\left(-2\right)=-4\) ; \(f\left(2\right)=8\)
Đồ thị hàm \(f\left(t\right)\):
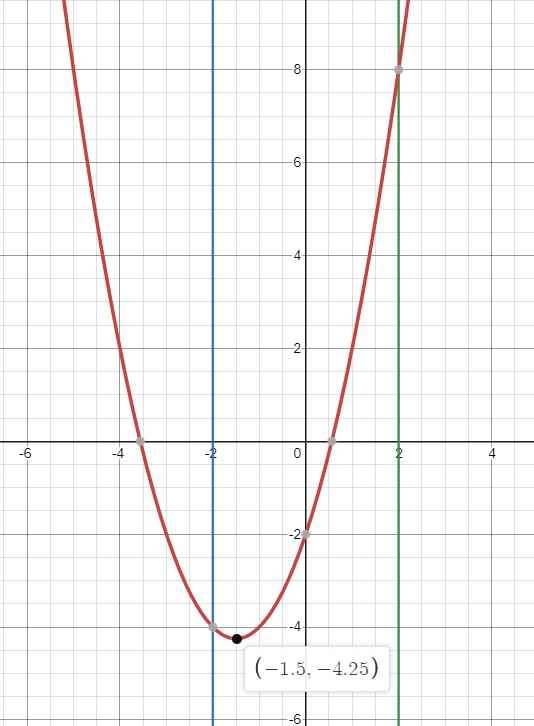
Từ đồ thị ta thấy \(y=-m\) cắt \(y=f\left(t\right)\) tại 2 điểm đều nằm ngoài \(\left[-2;2\right]\) khi và chỉ khi:
\(\left[{}\begin{matrix}-\dfrac{17}{4}< -m< -4\\-m>8\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}4< m< \dfrac{17}{4}\\m< -8\end{matrix}\right.\)
26 tháng 7 2021
thầy cho em hỏi làm mấy dạng tìm điều kiện này thạo thì nên học qua tư liệu nào ? Thầy có thể cho e một số file chuyên đề về mấy dạng này đc không?
e biết vẽ đồ thị của hàm \(\left(x-3\right)\left|x-1\right|\)dựa theo hàm số \(\left(x-3\right)\left(x-1\right)\)chưa nhỉ