Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}2x+3y+4=0\\3x+y-1=0\\2mx+5y-m=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+3y=-4\\3x+y=1\\2mx+5y-m=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x+9y=-12\\6x+2y=2\\2mx+5y-m=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}7y=-14\\3x+y=1\\2mx+5y-m=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-2\\3x=1-y=1-\left(-2\right)=3\\2mx+5y-m=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=-2\\x=1\\2mx+5y-m=0\end{matrix}\right.\)
Để hệ phương trình này có duy nhất 1 nghiệm thì thay x=1 và y=-2 vào 2mx+5y-m=0, ta được:
2m*1+5*(-2)-m=0
=>m-10=0
=>m=10

\(\Leftrightarrow x^2-2x-m+\dfrac{2\left(x^2-2x-m\right)\left(\sqrt{x}+1\right)}{x+\sqrt{2x+m}}=0\)
\(\Leftrightarrow\left(x^2-2x-m\right)\left(1+\dfrac{2\left(\sqrt{x}+1\right)}{x+\sqrt{2x+m}}\right)=0\)
\(\Leftrightarrow x^2-2x-m=0\)

Phương trình ax + b = 0 có nghiệm duy nhất khi a ≠ 0 .
Xét phương trình m 2 + 1 x + 2 = 0 có hệ số a= m2 + 1> 0 với mọi m.
Do đó, phương trình này luôn có nghiệm duy nhất với mọi giá trị của m.

a) mx2 – 2x – 4m – 1 = 0 (1)
Với m ≠ 0, ta có:
Δ’ = 1 + m.(4m + 1) = 4m2 + m + 1
= 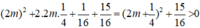 với mọi m.
với mọi m.
Hay phương trình (1) có hai nghiệm phân biệt với mọi m ≠ 0.
b) x = -1 là nghiệm của phương trình (1)
⇔ m.(-1)2 – 2.(-1) – 4m – 1 = 0
⇔ m + 2 - 4m = 0
⇔ -3m + 1 = 0
⇔ m = 1/3.
Vậy với m = 1/3 thì phương trình (1) nhận -1 là nghiệm.
Khi đó theo định lý Vi-et ta có: x2 + (-1) = 2/m (x2 là nghiệm còn lại của (1))
⇒ x2 = 2/m + 1= 6 + 1 = 7.
Vậy nghiệm còn lại của (1) là 7.

2x² - 3x + 2 = (1/8)(16x² - 24x + 9) + 7/8 = (1/8)(4x - 3)² + 7/8 > 0 nên |2x² - 3x + 2| = 2x² - 3x + 2
|2x² - 3x + 2| = 5m - 8x - 2x²
⇔ 2x² - 3x + 2 = 5m - 8x - 2x²
⇔ 4x² + 5x + 2 - 5m = 0
Để PT có nghiệm duy nhất thì đó phải là nhiệm kép :
Δ = 25 - 16(2 - 5m) = 80m - 7 = 0 ⇔ m = 7/80

Ta có: x 3 − 2 m + 1 x 2 + 4 m − 1 x − 2 m + 1 = 0 1
⇔ x − 1 x 2 − 2 m x + 2 m − 1 = 0 ⇔ x = 1 x 2 − 2 m x + 2 m − 1 ( * )
Để phương trình (1) có một nghiệm duy nhất thì pt (*) có nghiệm kép x = 1
⇔ Δ ' = m 2 − 2 m + 1 = 0 1 − 2 m + 2 m − 1 = 0 ⇔ m − 1 2 = 0 0 = 0 ⇔ m = 1
Đáp án cần chọn là: C
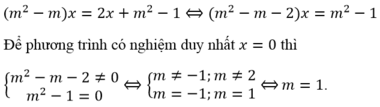
\(\left|2x-1\right|+\left|2x+1\right|=m\) (1)
Xét 3 trường hợp: \(x< -\frac{1}{2}\), \(-\frac{1}{2}\le x< \frac{1}{2}\) và \(x\ge\frac{1}{2}\).
Trường hợp 1: \(x< -\frac{1}{2}\Rightarrow\left\{{}\begin{matrix}\left|2x-1\right|=1-2x\\\left|2x+1\right|=-1-2x\end{matrix}\right.\)
Phương trình (1) tương đương
\(1-2x-1-2x-m=0\)
\(\Leftrightarrow-4x=m\)
Phương trình trên có nghiệm x duy nhất thỏa mãn điều kiện \(\Leftrightarrow m>2\). (2)
Trường hợp 2: \(-\frac{1}{2}\le x< \frac{1}{2}\Rightarrow\left\{{}\begin{matrix}\left|2x-1\right|=1-2x\\\left|2x+1\right|=2x+1\end{matrix}\right.\)
Phương trình (1) tương đương:
\(1-2x+1+2x-m=0\)
\(\Leftrightarrow-m=-2\)
Phương trình trên có vô số nghiệm khi và chỉ khi m = 2 (3).
Trường hợp 3: \(x\ge\frac{1}{2}\Rightarrow\left\{{}\begin{matrix}\left|2x-1\right|=2x-1\\\left|2x+1\right|=2x+1\end{matrix}\right.\).
Phương trình (1) tương đương:
\(2x-1+2x+1-m=0\)
\(\Leftrightarrow4x=m\)
Phương trình có nghiệm duy nhất \(\Leftrightarrow m>2\) (4)
Như vậy, kết hợp (2), (3) và (4) ta thấy:
- Với m = 2 thì phương trình có vô số nghiệm.
- Với m > 2 thì phương trình có 2 nghiệm phân biệt.
- Với m < 2 thì phương trình vô nghiệm.
Vậy không có m thỏa mãn phương trình (1) có nghiệm duy nhất.
Cảm ơn ạ