
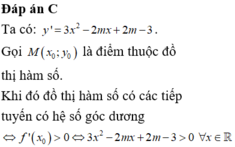
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

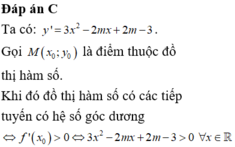

- Phương trình hoành độ giao điểm của d và (C) là
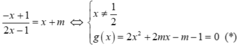
- Theo định lí Viet ta có x1+x2=-m; ![]()
Giả sử A( x1; y1); B( x2; y2).
- Ta có 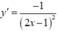 nên tiếp tuyến của (C) tại A và B có hệ số góc lần lượt là
nên tiếp tuyến của (C) tại A và B có hệ số góc lần lượt là 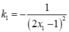 và
và 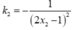 .Vậy
.Vậy
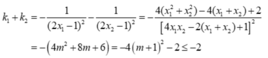
- Dấu "=" xảy ra khi và chỉ khi m= -1.
Vậy k1+ k2 đạt giá trị lớn nhất bằng -2 khi m= -1.
Chọn A.

+ Phương trình hoành độ giao điểm của d và (C) là
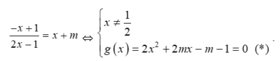
+ Theo định lí Viet ta có x1+ x2= -m ; x1.x2= ( -m-1) /2.
Gọi A( x1; y1) ; B( x2: y 2) .
+ Ta có y ' = - 1 ( 2 x - 1 ) 2 , nên tiếp tuyến của ( C) tại A và B có hệ số góc lần lượt là
k 1 = - 1 ( 2 x 1 - 1 ) 2 ; k 2 = - 1 ( 2 x 2 - 1 ) 2

Dấu "=" xảy ra khi và chỉ khi m= -1.
Vậy k1+ k2 đạt giá trị lớn nhất bằng - 2 khi m= -1.
Chọn B.

Ta có \(\overrightarrow{n}=\left(2;1\right)\) là vecto pháp tuyến của đường thẳng d
\(y'=3x^2-2\left(m+2\right)x+m-1\Rightarrow y'\left(1\right)=3-2m-4+m-1=-m-2\)
Gọi \(\Delta\) là tiếp tuyến của đồ thị hàm số (1) tại điểm có hoành độ bằng 1. Suy ra phương trình của \(\Delta\) có dạng \(y=y'\left(1\right)\left(x-1\right)+y\left(1\right)\)
Do đó \(\overrightarrow{n}=\left(m+2;1\right)\) là vecto pháp tuyến của \(\Delta\)
Theo đề bài ta có : \(\left|\cos\left(\overrightarrow{n_1.}\overrightarrow{n_2}\right)\right|=\cos30^0\Rightarrow\frac{\left|\overrightarrow{n_1.}\overrightarrow{n_2}\right|}{\left|\overrightarrow{n_1}\right|\left|\overrightarrow{n_2}\right|}=\frac{\sqrt{3}}{2}\)
\(\Leftrightarrow\frac{\left|2\left(m+2\right)+1\right|}{\sqrt{5}\sqrt{\left(m+2\right)^2+1}}=\frac{\sqrt{3}}{2}\)
\(\Leftrightarrow m^2+20m+25=0\)
\(\Leftrightarrow m=-10\pm5\sqrt{3}\)

a) Ta có : \(y'=3x^2+2\left(m-1\right)x+m\left(m-3\right)\)
Hàm số (1) có cực đại và cực tiểu nằm 2 phía đối với trục tung <=> phương trình : \(3x^2+2\left(m-1\right)x+m\left(m-3\right)=0\) có 2 nghiệm phân biệt trái dấu
\(\Leftrightarrow P< 0\Leftrightarrow m\left(m-3\right)< 0\Leftrightarrow0< m< 3\)
Vậy \(0< m< 3\) là giá trị cần tìm
b) Khi m = 1 ta có : \(y=x^3-2x\).
Gọi \(M\left(a;a^3-2a\right)\in\left(C\right),a\ne0\)
Ta có \(y'=3x^2-2\) nên hệ số góc của \(\Delta\) là \(y'\left(a\right)=3a^2-2\)
Ta có \(\overrightarrow{OM}\left(a;a^3-2a\right)\) nên hệ số góc đường thẳng OM là \(k=a^2-2\)
Do đó : \(\Delta\perp OM\Leftrightarrow y'_a.k=-1\)
\(\Leftrightarrow\left(3a^2-2\right)\left(a^2-2\right)=-1\Leftrightarrow3a^4-8a^2+5=0\)
\(M_1\left(1;-1\right);M_1\left(-1;1\right);M_3\left(-\frac{\sqrt{15}}{3};\frac{\sqrt{15}}{9}\right);M_4\left(\frac{\sqrt{15}}{3};-\frac{\sqrt{15}}{9}\right)\) \(\Leftrightarrow\left[\begin{array}{nghiempt}a^2=1\\a^2=\frac{5}{3}\end{array}\right.\) \(\Leftrightarrow\left[\begin{array}{nghiempt}a=\pm1\\a=\pm\frac{\sqrt{5}}{3}\end{array}\right.\)(Thỏa mãn)
Suy ra có 4 điểm thỏa mãn đề bài :\(M_1\left(1;-1\right);M_2\left(-1;1\right);M_3\left(-\frac{\sqrt{15}}{3};\frac{\sqrt{15}}{9}\right);M_4\left(\frac{\sqrt{15}}{3};-\frac{\sqrt{15}}{9}\right)\)

a. Tiếp tuyến của \(\left(C_m\right)\) tại điểm có hoành độ x = 1 có phương trình :
\(y=\left(m-2\right)\left(x-1\right)+3m-2=\left(m-2\right)x+3m\)
Yêu cầu của bài toán khi và chỉ khi \(\begin{cases}m-2=3\\2m\ne10\end{cases}\) vô nghiệm
Vậy không tồn tại m thỏa mãn yêu cầu bài toán
b. Ta có \(y'=3\left(x^2-\frac{4}{3}x+\frac{4}{9}\right)+m-\frac{7}{3}=3\left(x-\frac{2}{3}\right)^2+m-\frac{7}{3}\)
Suy ra \(y'\ge m-\frac{7}{3}\)
Tiếp tuyến tại điểm có hoành độ \(x=\frac{2}{3}\) có hệ số góc nhỏ nhất và hệ số góc có giá trị \(k=m-\frac{7}{3}\)
Yêu cầu bài toán \(\Leftrightarrow k.2=-1\Leftrightarrow\left(m-\frac{7}{3}\right).2=-1\Leftrightarrow m=\frac{11}{6}\)

Đường tròn (S) tâm \(I\left(-1;-3\right)\) bán kính \(R=3\)
Thế tọa độ A vào pt (S) thỏa mãn nên A nằm trên đường tròn
Ta cần tìm B, C sao cho chi vi ABC lớn nhất
Đặt \(\left(AB;AC;BC\right)=\left(c;b;a\right)\Rightarrow\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}=2R\)
\(\Rightarrow a+b+c=2R\left(sinA+sinB+sinC\right)\)
Mặt khác ta có BĐT quen thuộc \(sinA+sinB+sinC\le\dfrac{3\sqrt{3}}{2}\)
Dấu "=" xảy ra khi tam giác ABC đều
\(\Rightarrow a=b=c=2R.sin60^0=3\sqrt{3}\)
Khi đó I đồng thời là trọng tâm kiêm trực tâm \(\Rightarrow\left\{{}\begin{matrix}BC\perp AI\\d\left(A;BC\right)=\dfrac{a\sqrt{3}}{2}=\dfrac{9}{2}\end{matrix}\right.\)
\(\Rightarrow\) Phương trình BC có dạng \(y=-\dfrac{3}{2}\)
Hay (Cm) có 1 tiếp tuyến là \(y=-\dfrac{3}{2}\) (hệ số góc bằng 0 nên tiếp tuyến này đi qua 2 cực tiểu)
\(\Rightarrow m=-1\)

Ta có : \(y'=3x^2-2\left(m-1\right)x+3m+1\)
Gọi \(M\left(x_0;y_0\right)\) là tiếp điểm, ta có : \(x_0=1\Rightarrow y_0=3m+1,y'\left(1\right)=m+6\)
Phương trình tiếp tuyến tại M : \(y=\left(m+6\right)\left(x-1\right)+3m+1\)
Tiếp tuyến đi qua A \(\Leftrightarrow-1=m+6+3m+1\Leftrightarrow m=-2\)
Vậy m = -2 là giá trị cần tìm

a)
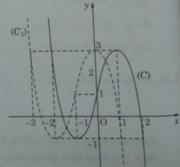
b) Tịnh tiến (C) song song với trục Ox sang trái 1 đơn vị, ta được đồ thị (C1) của hàm số.
y = f(x) = − ( x + 1 ) 3 + 3(x + 1) + 1 hay f(x) = − ( x + 1 ) 3 + 3x + 4 (C1)
Lấy đối xứng (C1) qua trục Ox, ta được đồ thị (C’) của hàm số y = g(x) = ( x + 1 ) 3 − 3x – 4
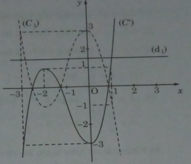
c) Ta có: ( x + 1 ) 3 = 3x + m (1)
⇔ ( x + 1 ) 3 − 3x – 4 = m – 4
Số nghiệm của phương trình (1) là số giao điểm của hai đường :
y = g(x) = ( x + 1 ) 3 − 3x – 4 (C’) và y = m – 4 (d1)
Từ đồ thị, ta suy ra:
+) m > 5 hoặc m < 1: phương trình (1) có một nghiệm.
+) m = 5 hoặc m = 1 : phương trình (1) có hai nghiệm.
+) 1 < m < 5 , phương trình (1) có ba nghiệm.
d) Vì (d) vuông góc với đường thẳng:
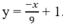
nên ta có hệ số góc bằng 9.
Ta có: g′(x) = 3 ( x + 1 ) 2 – 3
g′(x) = 9 ⇔ 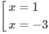
Có hai tiếp tuyến phải tìm là:
y – 1 = 9(x – 1) ⇔ y = 9x – 8;
y + 3 = 9(x + 3) ⇔ y = 9x + 24.