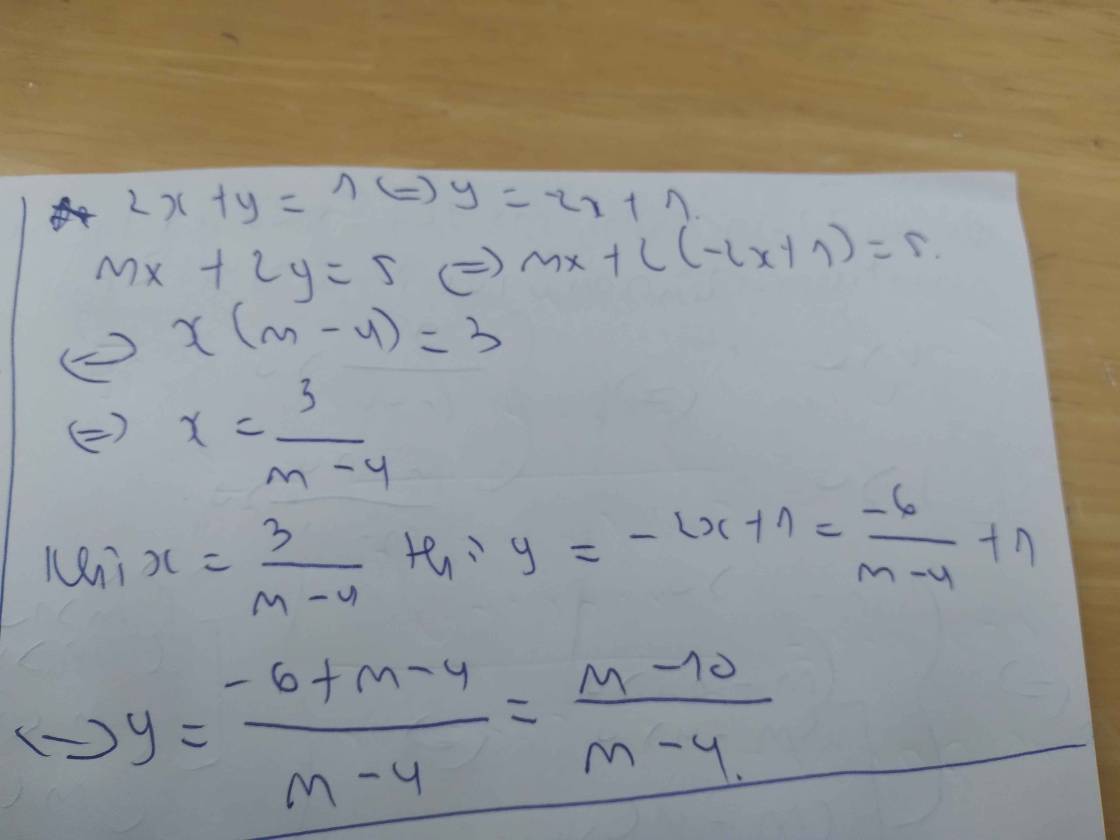Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

m x + 2 y = 5 ⇒ y = − m 2 x + 5 2
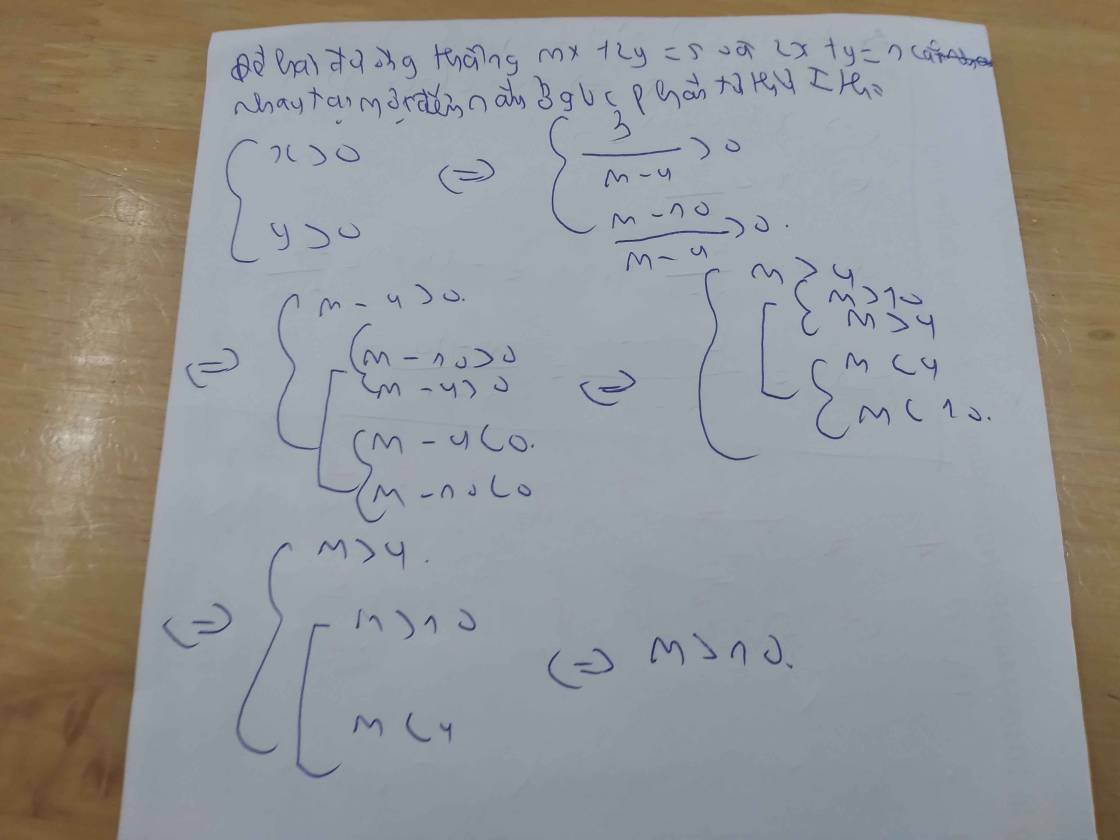
d ∩ d ’ ⇔ − m 2 ≠ − 2 ⇔ m ≠ 4
Xét phương trình hoành độ giao điểm của d và d’
− m 2 x + 5 2 = − 2 x + 1 ⇔ 4 − m 2 x = − 3 2 ⇔ x = 3 m − 4 ⇒ y = − 2 . 3 m − 4 − 1 = m − 10 m − 4
Do d cắt d’ tại điểm nằm ở góc phần tư thứ nhất nên ta có:
x > 0 y > 0 ⇔ 3 m − 4 > 0 m − 10 m − 4 > 0 ⇔ m > 4 m > 10 ⇔ m > 10
Kết hợp điều kiện suy ra m > 10 thỏa mãn yêu cầu đề bài
Đáp án cần chọn là: C

a: Thay m=3 vào (d), ta được:
y=3x-3+1=3x-2
Tọa độ giao điểm của (P) và (d) là:
\(\left\{{}\begin{matrix}x^2-3x+2=0\\y=x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(x-2\right)=0\\y=x^2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(1;1\right);\left(2;4\right)\right\}\)
b: Phương trình hoành độ giao điểm là:
\(x^2-mx+m-1=0\)
Để (P) cắt (d) tại hai điểm về hai phía của trục tung thì m-1<0
hay m<1
c: Để (P) cắt (d) tại hai điểm phân biệt có hoành độ dương thì
\(\left\{{}\begin{matrix}\left(-m\right)^2-4\left(m-1\right)>0\\m>0\\m-1>0\end{matrix}\right.\Leftrightarrow m>1\)

a) Gọi A(xA;yA) là điểm cố định mà (d) luôn đi qua
=> yA = mxA + 1 với mọi m
=> xA.m + 1 - yA = 0 với mọi m
<=> xA = 0 và 1 - yA = 0
<=> xA = 0 ; yA = 1
Vậy A(0;1)
b) Phương trình hoành đọ giao điểm của (P) và (d) là:
x2 = mx + 1
<=> x2 - mx - 1 = 0
\(\Delta\) = (-m)2 + 4 = m2 + 4 > 0 với mọi m
=> Pt có 2 nghiệm pb với mọi m
=> (P) luôn cắt (d) tại 2 điểm phân biệt A;B
Theo Vi - et ta có: xAxB = -1 < 0
=> xA ; xB trái dấu => A; B nằm khác phía so với trục tung