Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nhìn biểu thức có vẻ rối, nhưng ta chẳng cần quan tâm cái biến làm gì cả.
Coi như không có biến, ta có :
\(1+3+5+...+\left(2k-1\right)=3249\)
\(\Rightarrow\dfrac{\dfrac{\left(2k-1\right)-1}{2}+1}{2}\cdot\left(2x-1+1\right)=3249\)
\(\Rightarrow CALC\left(k\right)=57\)
Vậy \(k=57\)

\(x^3y^5+3x^3y^5+...+\left(2k-1\right)x^3y^5=3249x^3y^5\)
\(\Leftrightarrow x^3y^5\left[1+2+3+...+\left(2k-1\right)\right]=3249x^3y^5\)
\(\Leftrightarrow1+3+5+...+\left(2k-1\right)=3249\)
\(\Leftrightarrow\frac{\left[\left(2k-1\right)+1\right].\left(\frac{\left(2k-1\right)-1}{2}+1\right)}{2}=3249\)
\(\Leftrightarrow\frac{2k.\left(k-1+1\right)}{2}=3249\)
\(\Leftrightarrow\frac{2k^2}{2}=3249\)
\(\Leftrightarrow k^2=3249=57^2\) ( ko xét k = - 57 vì theo quy luật thi k luôn dương )
\(\Rightarrow k=57\)

Ta có:\(x^3y^5+3x^3y^5+5x^3y^5+...+\left(2k-1\right)x^3y^5=3249x^3y^5\)
\(x^3y^5\left(1+3+5+...+2k-1\right)=3249x^3y^5\)
\(\Rightarrow1+3+5+...+2k-1=3249\)
\(\Rightarrow\frac{\left(\frac{2k-1-1}{2}+1\right).\left(2k-1+1\right)}{2}=3249\)
\(\Rightarrow\frac{k.2k}{2}=3249\)
\(\Rightarrow k^2=3249\)
\(\Rightarrow k=57\) hoặc k=-57
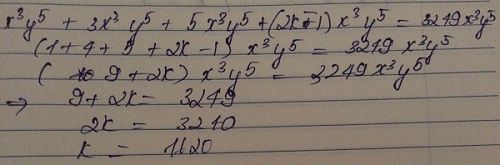
sorry mình ghi nhầm :) k = 57 mới đúng
k = 58