Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{2}\)=\(\dfrac{y}{5}\)=\(\dfrac{x+y}{2+5}\)=\(\dfrac{-21}{7}\)=-3
=>\(\dfrac{x}{2}\)=\(\dfrac{y}{5}\)=5x=2y
=>x=5.-3=-15
=>y=2.-3=-6
Vậy x=-15;y=6

\(\frac{x}{2}=\frac{y}{3};\frac{y}{4}=\frac{z}{5}\)và x + y -z = 10
\(\frac{x}{2}=\frac{y}{3}=\frac{1}{4}.\frac{x}{2}=\frac{1}{4}.\frac{y}{3}\)\(=\frac{x}{8}=\frac{y}{12}\)
\(\frac{y}{4}=\frac{z}{5}=\frac{1}{3}.\frac{y}{4}=\frac{1}{3}.\frac{z}{5}=\frac{y}{12}=\frac{z}{15}\)
\(\Leftrightarrow\frac{x}{8}=\frac{y}{12}=\frac{z}{15}\)và x + y - z = 10
Theo tính chất dãy tỉ số bằng nhau:
\(\frac{x}{8}=\frac{y}{12}=\frac{z}{15}=\frac{x+y-z}{8+12-15}=\frac{10}{5}=2\)
* \(\frac{x}{8}=2\Rightarrow x=2.8=16\)
* \(\frac{y}{12}=2\Rightarrow y=2.12=24\)
* \(\frac{z}{5}=2\Rightarrow z=2.5=10\)
Vậy...
Ý mk nhầm chút xíu nhé! Cko sorry!
* \(\frac{z}{15}=2\Rightarrow z=2.15=30\)
... :( Xl

2). Ta có: x/2=y/3 => x/8 = y/12
y/4=z/5 => y/12 = z/15
=> x/2=y/12=z/15 và x+y-z=10
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{2}\)=\(\frac{y}{12}\)=\(\frac{z}{15}\)=\(\frac{x+y-z}{2+12-15}\)=\(\frac{10}{-1}\)= -10
=> x=2.(-10)=-20
y=12.(-10)=-120
z=15.(-10)=-150
Vậy x=-20; y=-120;z=-150
3). Đặt \(\frac{x}{2}\)=\(\frac{y}{5}\)= k
=> x=2k
y=5k
Ta có xy = 10
2k.5k =10
10. k2=10
k2 = 10 :10=1
=> k =1; k=-1
+) k = 1
=> x=2.1=2
y=5.1=5
+) k = -1
=> x= 2.(-1) =-2
y=5.(-1) = -5
Vậy x=2;y=5 hoặc x=-2;y=-5
Câu 2:
Ta có \(\frac{x}{2}=\frac{y}{3}=\frac{x}{8}=\frac{y}{12}\)(1)
\(\frac{y}{4}=\frac{z}{5}=\frac{y}{12}=\frac{z}{15}\)(2)
Từ (1) và (2) suy ra:\(\frac{x}{8}=\frac{y}{12}=\frac{z}{15}\)
Áp dụng dãy tỉ số bằng nhau ta có:
\(\Rightarrow\)\(\frac{x}{8}=\frac{y}{12}=\frac{z}{15}=\frac{x+y-z}{8+12-15}=\frac{10}{5}=2\)
\(\Rightarrow\begin{cases}\frac{x}{8}=2\\\frac{y}{12}=2\\\frac{z}{15}=2\end{cases}\)\(\Rightarrow\begin{cases}x=16\\y=24\\z=30\end{cases}\)
Vậy x=16;y=24;z=30

Ta có
\(\frac{x}{2}=\frac{y}{5}=k\Rightarrow\hept{\begin{cases}x=2k\\y=5k\end{cases}}\)
\(\Rightarrow x\cdot y=2k\cdot5k=10\)
\(\Rightarrow k^2\cdot10=10\)
\(\Rightarrow k^2=1\)
\(\Rightarrow k^2=1^2\)
\(\Rightarrow k=1\)
Thay K=1 vào x;y ta có
\(\hept{\begin{cases}x=2k=2\\y=5k=5\end{cases}}\)
ti ck nha
\(\frac{x}{2}=\frac{y}{5}\Rightarrow\left(\frac{x}{2}\right)^2=\left(\frac{y}{5}\right)^2=\frac{x}{2}.\frac{y}{5}=\frac{x.y}{2.5}=\frac{10}{10}=1\)
\(\Rightarrow\hept{\begin{cases}x=2.1=2\\y=5.1=5\end{cases}}\)
Vậy x = 2, y = 5
P/s: Cô mình có dạy tính chất a = b => a2 = b2 = ab nên mình áp dụng theo

Ta có \(\frac{x+5}{2}=\frac{y-2}{3}\)và \(x-y=-10\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x+5}{2}=\frac{y-2}{3}=\frac{x+5-y-2}{2-3}=\frac{x-y+5-2}{2-3}=\frac{-10+5-2}{2-3}=\frac{-7}{-1}=7\)
=> \(\frac{x+5}{2}=7\)=> x + 5 = 14 => x = 9
và \(\frac{y-2}{3}=7\)=> y - 2 = 21 => y = 23

\(dat:\frac{x}{2}=\frac{y}{5}=k\)
x=2k ; y=5k
x.y=10k2
10 = 10k2
k2 = 1
k = +-1
Voi : k=1 = > x=1.2=2 ; y=5.1=5
voi : k=-1 => x=-1.2=-2 ; y=-1.5=-5
\(\frac{x}{2}=\frac{y}{3};\frac{y}{4}=\frac{z}{5}\Rightarrow\frac{x}{2}=\frac{4y}{12};\frac{3y}{12}=\frac{z}{5}\Rightarrow\frac{x}{8}=\frac{y}{12};\frac{y}{12}=\frac{z}{15}\Rightarrow\frac{x}{8}=\frac{y}{12}=\frac{z}{15}\)
Ap dung tinh chat day ti so bang nhau ta co :
\(\frac{x}{8}=\frac{y}{12}=\frac{z}{15}=\frac{x+y-z}{8+12-15}=\frac{10}{5}=2\)
Suy ra : \(\frac{x}{8}=2\Rightarrow x=16;\frac{y}{12}=2\Rightarrow y=2.12=24;\frac{z}{15}=2\Rightarrow z=2.15=30\)
nhieu qua lam ko het

Giải:
Đặt \(\dfrac{x}{2}=\dfrac{y}{5}=k\Rightarrow\left\{{}\begin{matrix}x=2k\\y=5k\end{matrix}\right.\)
Ta có: \(xy=10\)
\(\Rightarrow10k^2=10\)
\(\Rightarrow k^2=1\)
\(\Rightarrow k=\pm1\)
+) \(k=1\Rightarrow x=2,y=5\)
+) \(k=-1\Rightarrow x=-2;y=-5\)
Vậy...
Nhân cả hai vế của tỉ lệ thức \(\dfrac{x}{2}\) = \(\dfrac{y}{5}\) với x (x ≠ 0), ta được: ![]() Thay xy = 10, ta được: \(\dfrac{x^2}{2}\) = \(\dfrac{10}{5}\)= 2 ⇔x2 = 4. Do đó x = 2 hoặc x = -2
Thay xy = 10, ta được: \(\dfrac{x^2}{2}\) = \(\dfrac{10}{5}\)= 2 ⇔x2 = 4. Do đó x = 2 hoặc x = -2
Khi x = 2 thì y = 5
Khi x = -2 thì y = -5

Lời giải:
Theo tính chất của dãy tỉ số bằng nhau ta có:
Do đó
Vậy x=6, y =10

1/ a, Ta có :
\(x-2y+3z=35\)
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\)
\(\Leftrightarrow\dfrac{x}{3}=\dfrac{2y}{8}=\dfrac{3z}{15}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{3}=\dfrac{2y}{8}=\dfrac{3z}{15}=\dfrac{x-2y+3z}{3-8+15}=\dfrac{35}{10}=\dfrac{7}{2}\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{3}=\dfrac{7}{2}\Leftrightarrow x=\dfrac{21}{2}\\\dfrac{x}{4}=\dfrac{7}{2}\Leftrightarrow y=14\\\dfrac{z}{5}=\dfrac{7}{2}\Leftrightarrow z=\dfrac{35}{2}\end{matrix}\right.\)
Vậy ..
Đặt k = . Ta có x = 2k, y = 5k
. Ta có x = 2k, y = 5k
Từ xy=10. suy ra 2k.5k = 10 => 10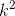 = 10 =>
= 10 => 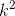 = 1 => k = ± 1
= 1 => k = ± 1
Với k = 1 ta được = 1 suy ra x = 2, y = 5
= 1 suy ra x = 2, y = 5
Với k = -1 ta được = -1 suy ra x = -2, y = -5
= -1 suy ra x = -2, y = -5
Gọi \(\dfrac{x}{2}=\dfrac{y}{5}=k\)
Với \(\dfrac{x}{2}=k\Rightarrow x=2k\); \(\dfrac{y}{5}=k\Rightarrow y=5k\)
Theo đề bài,ta còn có:
\(xy=10\)
hay 2k.5k=10
10k2 =10
\(\Rightarrow k=\pm1\)
Với k=1 \(\Rightarrow\dfrac{x}{2}=\dfrac{y}{5}=1\Rightarrow x=2;y=5\)
Với k=-1 \(\Rightarrow\dfrac{x}{2}=\dfrac{y}{5}=-1\Rightarrow x=-2;y=-5\)