Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


- Nếu u + v = -11 và uv = 18 thì u và v là hai nghiệm của phương trình \(x^2+11x+18=0\). Suy ra u = - 2, v = -9 hoặc u = -9; v = -2

a) u + v = 12; uv = 28 và u > v
u và v là hai nghiệm của phương trình:
x2 – 12x + 28 = 0
\(\Delta\)’ = 36 – 28 = 8
\(\Rightarrow x_1=6+2\sqrt{2}\)
\(x_2=6-2\sqrt{2}\)
Vì \(6+2\sqrt{2}>6-2\sqrt{2}\)
\(\Rightarrow u=6+2\sqrt{2}\)
\(v=6-2\sqrt{2}\)
b) u + v = 3; uv = 6
u và v là hai nghiệm của phương trình:
x2 – 3x + 6 = 0
\(\Delta\) = (-3)2 – 4.1.6 = 9 – 24 = -15 < 0
Phương trình vô nghiêmh suy ra không có 2 số u và v thỏa mãn điều kiện đã cho.

Ta có \(u^2+v^2=130\Leftrightarrow u^2+2uv+v^2=130+2uv\Leftrightarrow\left(u+v\right)^2=4\Leftrightarrow\)\(\left[{}\begin{matrix}u+v=2\\u+v=-2\end{matrix}\right.\)
* u+v=2\(\Leftrightarrow\left\{{}\begin{matrix}u+v=2\\uv=-63\end{matrix}\right.\)
Vậy u,v là 2 nghiệm của phương trình \(x^2-2x-63=0\Leftrightarrow\left(x-9\right)\left(x+7\right)=0\Leftrightarrow\)\(\left[{}\begin{matrix}x=9\\x=-7\end{matrix}\right.\)\(\Leftrightarrow\)\(\left[{}\begin{matrix}\left\{{}\begin{matrix}u=9\\v=-7\end{matrix}\right.\\\left\{{}\begin{matrix}u=-7\\v=9\end{matrix}\right.\end{matrix}\right.\)
* u+v=-2\(\Leftrightarrow\left\{{}\begin{matrix}u+v=-2\\uv=-63\end{matrix}\right.\)
Vậy u,v là 2 nghiệm của phương trình
\(x^2+2x-63=0\Leftrightarrow\left(x+9\right)\left(x-7\right)=0\Leftrightarrow\)\(\left[{}\begin{matrix}x=-9\\x=7\end{matrix}\right.\)\(\Leftrightarrow\)\(\left[{}\begin{matrix}\left\{{}\begin{matrix}u=-9\\v=7\end{matrix}\right.\\\left\{{}\begin{matrix}v=7\\u=-9\end{matrix}\right.\end{matrix}\right.\)
Vậy (u;v)={(9;-7);(-7;9);(-9;7);(7;-9)}


Mất 1 tiếng sau khi nhìn cái đề mới giải đc
Ta có \({u+v}≥ 2uv\)
\(=>{(u+v)^2-2uv}≥2uv\)
\(<=>{(u+v)^2/ 2}≥ 2uv\)
Và \({(u+v)^2/4}≥uv\)
\(P= {u^2+v^2}+{33 \over uv}\)
\(≥ {2uv}+{33\over uv}\)
\(={(u+v)^2 \over 2}+{33/{(u+v)^2 \over 4}}\)
Thế số vào ta sẽ đc kết quả \({65 \over 4}\)
Vậy GTNN của P là 65/4 khi u=v = 2
Sai!
Ta có \(P=u^2+v^2+\frac{33}{uv}\)
\(\ge\frac{\left(u+v\right)^2}{2}+\frac{33}{\frac{\left(u+v\right)^2}{4}}\)
\(=\frac{4^2}{2}+\frac{33}{\frac{4^2}{4}}=\frac{65}{4}\)
"=" <=> u=v=2

Câu a em nghĩ có thể làm như vầy ạ,câu b để sau (em mới lớp 7,cần suy ra nghĩ thêm)
a)ĐKXĐ: x > 4; \(y\ne2\)
Đặt \(\frac{1}{\sqrt{x-4}}=a;\frac{1}{y+2}=b\)
Hệ phương trình trở thành: \(\hept{\begin{cases}3a+4b=7\\5a-b=4\end{cases}}\Leftrightarrow\hept{\begin{cases}3a+4b=7\\20a-4b=16\end{cases}}\)
Cộng theo vế với vế của hai phương trình trong hệ,ta được: \(23a=7+16=23\Rightarrow a=1\Rightarrow b=1\)
Đến đây dễ rồi ạ.

a) S = 32 ; P = 231 ⇒ S 2 – 4 P = 322 – 4 . 231 = 100 > 0
⇒ Tồn tại u và v là hai nghiệm của phương trình: x 2 – 32 x + 231 = 0 .
Ta có: Δ = ( - 32 ) 2 – 4 . 231 = 100 > 0
⇒ PT có hai nghiệm:
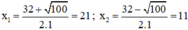
Vậy u = 21 ; v = 11 hoặc u = 11 ; v = 21.
b) S = -8; P = -105 ⇒ S 2 – 4 P = ( - 8 ) 2 – 4 . ( - 105 ) = 484 > 0
⇒ u và v là hai nghiệm của phương trình: x 2 + 8 x – 105 = 0
Ta có: Δ ’ = 4 2 – 1 . ( - 105 ) = 121 > 0
Phương trình có hai nghiệm:
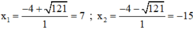
Vậy u = 7 ; v = -15 hoặc u = -15 ; v = 7.
c) S = 2 ; P = 9 ⇒ S 2 – 4 P = 2 2 – 4 . 9 = - 32 < 0
⇒ Không tồn tại u và v thỏa mãn.
Hai số u và v với u 2 + v 2 =85 và uv =18 suy ra : u 2 v 2 =324 nên u 2 và v 2 là nghiệm của phương trình x 2 -85x +324 =0
∆ = - 85 2 – 4.1.324= 7225 – 1296=5929 > 0
∆ = 2959 =77
Ta có: u 2 =81 , v 2 =4 suy ra: u = ± 9 ,v= ± 2
hoặc u 2 =4 , v 2 =81 suy ra: u = ± 2 ,v= ± 9
Vậy nếu u=9 thì v=2 hoặc u=-9 ,v=-2
nếu u=2 thì v=9 hoặc u= -2 ,v=-9