Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bạn có: a^3 + b^3 = (a + b)(a^2 - ab + b^2) = 28(a^2 - ab + b^2)
theo đề bài , bạn có: a + b = 28 >= 2√ab (bất đẳng thức AM-GM)
=> 28 >= 2√ab
hay 14 >= √ab => 196 >=ab hay -ab >= -196
đồng thời bạn có (a + b)^2 = 784
suy ra a^2 + 2ab + b^2 = 784
suy ra a^2 + 2ab + b^2 - 3ab = 784 - 3ab
hay a^2 -ab + b^2 >= 784 - 588
hay a^2 - ab + b^2 >= 196
suy ra bạn có P = a^3 + b^2 = (a+b)(a^2 - ab +b^2) = 28(a^2 - ab + b^2) >= 28.196 = 5488
=> min P = 5488 <=> a = b = 14

a) Vì nên (n + 1) ∈ Ư(6) = {1; 2; 3; 6}
Ta có bảng sau:
n + 1 | 1 | 2 | 3 | 6 |
n | 0 | 1 | 2 | 5 |
Vì n là số tự nhiên nên n ∈ {0; 1; 2; 5}
Vậy n ∈ {0; 1; 2; 5}.
b) Gọi x = 23.3a và y = 2b.35
Ta có tích của hai số là tích của ƯCLN và BCNN của hai số đó.
Ta có: x. y = ƯCLN(x, y). BCNN(x, y)
Vì ước chung lớn nhất của hai số là và bội chung nhỏ nhất của hai số là 23.36.
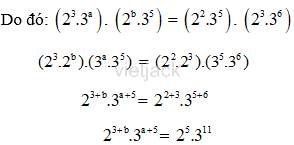
Vì thế 3 + b = 5. Suy ra b = 5 – 3 = 2
a + 5 = 11. Suy ra a = 11 – 5 = 6
Vậy a = 6; b = 2.
Gọi x = 23.3a và y = 2b.35
Ta có: x. y = ƯCLN(x, y). BCNN(x, y)
Vì ước chung lớn nhất của hai số là 22.35 và bội chung nhỏ nhất của hai số là 23.36
Ta được x.y= 22.35.23.36=22.23.35.36=25.31122.35.23.36=22.23.35.36=25.311
Mà xy =23+b.3a+523+b.3a+5
Ta được 5=3+b và 11=a+5
Vậy b=2 và a=6

a: \(n+1\in\left\{1;2;3;6\right\}\)
hay \(n\in\left\{0;1;2;5\right\}\)

a: \(\Leftrightarrow n+1\in\left\{1;2;3;6\right\}\)
hay \(n\in\left\{0;1;2;5\right\}\)

a. Vậy hai số có UCLN đạt giá trị lớn nhất là 50 , 25
b. Vậy hai số có BCNN đạt giá trị lớn nhất là 50 , 49
71;95