Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi chiều dài là a, chiều rộng là b.
Nửa chu vi hình chữ nhật là : \(\dfrac{94,4}{2}=47,2\left(m\right)\)
Ta có hệ pt : \(\left\{{}\begin{matrix}a+b=47,2\\a\cdot b=494,55\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=47,2-b\\\left(47,2-b\right)\cdot b=494,55\end{matrix}\right.\)
\(\left\{{}\begin{matrix}a=47,2-b\\47,2b-b^2=494,55\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=47,2-15,7=31,5\\b=15,7\left(giải-HPT-bậc-2\right)\end{matrix}\right.\)
Vậy chiều dài là 31,5 mét, chiều rộng 15,7 mét.
b) Vẫn gọi chiều dài là a, chiều rộng là b.
Có hpt : \(\left\{{}\begin{matrix}a-b=12,1\\a\cdot b=1089\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=12,1+b\\\left(12,1+b\right)\cdot b=1089\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=12,1+b\\12,1b+b^2=1089\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=12,1+27,5=39,6\\b=27,5\left(Giải-HPT-Bậc-2\right)\end{matrix}\right.\)
Vậy chiều dài là 39,6 mét, chiều rộng là 27,5 mét.

Đáp án: A
Gọi chiều dài, chiều rộng của mảnh vườn lần lượt là ![]() (m)
(m) ![]()
Theo đề bài ta có:
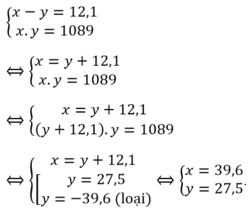

Gọi 2 cạch của HCN lần lượt là a và b (a<b)
\(\Rightarrow\frac{a}{4}=\frac{b}{7};ab=112\)
\(\Rightarrow\frac{a^2}{16}=\frac{b^2}{49}=\frac{a.b}{4.7}=\frac{112}{28}=4\)
\(\Rightarrow\begin{cases}a=\pm8\\b=\pm14\end{cases}\)
Mà a;b>0
\(\Rightarrow\begin{cases}a=8\\b=14\end{cases}\)
Vậy các cạnh của HCN là 8cm và 14cm

a) Mỗi hình vuông là một hình thoi (có một góc vuông). Vậy A ⊂ B, A ≠ B.
b) Mỗi số là ước của 6 là một ước chung của 24 và 30.
n ∈ B => n ∈ A. Vậy B ⊂ A. Mặt khác mỗi ước chung của 24 và 30 là một ước của 6. Vậy A ⊂ B. Suy ra A= B.
a) Mỗi hình vuông là một hình thoi (có một góc vuông). Vậy A ⊂ B, A ≠ B.
b) Mỗi số là ước của 6 là một ước chung của 24 và 30.
n ∈ B => n ∈ A. Vậy B ⊂ A. Mặt khác mỗi ước chung của 24 và 30 là một ước của 6. Vậy A ⊂ B. Suy ra A= B.






Gọi chiều dài, chiều rộng của mảnh vườn hình chữ nhật lần lượt là x (m), y (m). (điều kiện x > y > 0)
a) Theo đề bài:
Chu vi là 94,4m nên ta có phương trình: 2(x + y) = 94,4 (1)
Diện tích là 494,55m2 nên ta có phương trình: x.y = 494,55 (2)
Từ (1) và (2) ta có hệ:
Giải hệ phương trình trên:
Cách 1: Dựa vào định lý Vi–et đảo
Từ hệ phương trình suy ra x, y là nghiệm của phương trình:
X2 – 47,2X + 494,55 = 0
Giải phương trình ta được: X1 = 31,5 và X2 = 15,7
Vì x > y nên x = 31.5 và y = 15.7
Cách 2: Phương pháp thế
Từ x + y = 47,2 ⇒ x = 47,2 – y, thay vào phương trình x.y = 494,55 ta được:
(47,2 – y).y = 494,55
⇔ 47,2.y – y2 = 494,55
⇔ y2 – 47,2y + 494,55 = 0
⇔ y = 31.5 hoặc y = 15.7
Nếu y = 31.5 ⇒ x = 15.7 (loại vì x < y)
Nếu y = 15.7 ⇒ x = 31.5 (thỏa mãn).
Vậy hình chữ nhật có chiều dài bằng 31.5m và chiều rộng bằng 15.7m
b) Theo đề bài:
Hiệu của hai cạnh là 12,1 m nên ta có phương trình: x – y = 12,1 (3)
Diện tích là 1089m2 nên ta có phương trình: x.y = 1089 (4)
Từ (3) và (4) ta có hệ: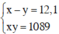
Từ (3) ⇒ x = 12,1 + y, thay vào (4) ta được:
(12,1 + y).y = 1089
⇔ y2 + 12,1.y – 1089 = 0
⇔ y = 27,5 (t/m) hoặc y = –39,6 (loại)
⇒ x = 12,1 + 27,5 = 39,6
Vậy hình chữ nhật có chiều dài 39,6m và chiều rộng 27,5m