Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\dfrac{\left(x-1\right)^2}{x-2}=\dfrac{\left(x-2\right)^2+2\left(x-2\right)+1}{x-2}=x-2+2+\dfrac{1}{x-2}\ge2+2\sqrt{\left(x-2\right).\dfrac{1}{x-2}}=4\)
GTNN là 4 khi x=3

\(f\left(-2\right)-f\left(1\right)=\left(-2\right)^2+2+\sqrt{2-\left(-2\right)}-\left(1^2+2+\sqrt{2-1}\right)\) \(=8-4=4\).
\(f\left(-7\right)-g\left(-7\right)=\left(-7\right)^2+2+\sqrt{2-\left(-7\right)}-\left(-2.\left(-7\right)^3-3.\left(-7\right)+5\right)=-658\)

a) Ta lập bảng xét dấu
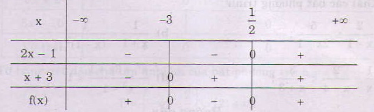
Kết luận: f(x) < 0 nếu - 3 < x <
f(x) = 0 nếu x = - 3 hoặc x =
f(x) > 0 nếu x < - 3 hoặc x > .
b) Làm tương tự câu a).
f(x) < 0 nếu x ∈ (- 3; - 2) ∪ (- 1; +∞)
f(x) = 0 với x = - 3, - 2, - 1
f(x) > 0 với x ∈ (-∞; - 3) ∪ (- 2; - 1).
c) Ta có: f(x) =
Làm tương tự câu b).
f(x) không xác định nếu x = hoặc x = 2
f(x) < 0 với x ∈ ∪
f(x) > 0 với x ∈ ∪ (2; +∞).
d) f(x) = 4x2 – 1 = (2x - 1)(2x + 1).
f(x) = 0 với x =
f(x) < 0 với x ∈
f(x) > 0 với x ∈ ∪

a: ĐKXĐ: \(\left(2x^2-5x+2\right)\left(x^3+1\right)< >0\)
=>(2x-1)(x-2)(x+1)<>0
hay \(x\notin\left\{\dfrac{1}{2};2;-1\right\}\)
b: ĐKXĐ: x+5<>0
=>x<>-5
c: ĐKXĐ: x4-1<>0
hay \(x\notin\left\{1;-1\right\}\)
d: ĐKXĐ: \(x^4+2x^2-3< >0\)
=>\(x\notin\left\{1;-1\right\}\)

Vì 3 ≤ x ≤ 7 => x - 3 ≥ 0; 7 - x ≥ 0
=> C ≥ 0
Dấu = xảy ra khi và chỉ khi x = 3 hoặc x = 7
C = (x - 3)(7 - x) ≤ \(\dfrac{1}{4}\)(x - 3 + 7 - x)2 = \(\dfrac{1}{4}\).42 = 4
Dấu "=" xảy ra <=> x - 3 = 7 - x <=> x = 5
\(G=\left(x^2+\sqrt[3]{3}\right)+\left(\dfrac{2}{x^3}+\dfrac{2}{\sqrt{3}}+\dfrac{2}{\sqrt{3}}\right)-\sqrt[3]{3}-\dfrac{4}{\sqrt{3}}\ge2\sqrt{x^2.\sqrt[3]{3}}+3\sqrt[3]{\dfrac{2}{x^3}.\dfrac{2}{\sqrt{3}}.\dfrac{2}{\sqrt{3}}}-\sqrt[3]{3}-\dfrac{4}{\sqrt{3}}=2\sqrt[6]{3}.x+\dfrac{6}{\sqrt[3]{3}x}-\sqrt[3]{3}-\dfrac{4}{\sqrt{3}}\ge2\sqrt{2\sqrt[6]{3}.x.\dfrac{6}{\sqrt[3]{3}x}}-\sqrt[3]{3}-\dfrac{4}{\sqrt{3}}=2\sqrt{\dfrac{12\sqrt[6]{3}}{\sqrt[3]{3}}}-\sqrt[3]{3}-\dfrac{4}{\sqrt{3}}\)
Dấu "=" xảy ra khi và chỉ khi \(x=\sqrt[6]{3}\)

a) 3x^3 -10x+3 =(3x-1)(x-3)
| x | -vc | 1/3 | 5/4 | 3 | +vc | |||||||||
| 3x-1 | - | 0 | + | + | + | + | + | |||||||
| x-3 | - | - | - | - | - | 0 | + | |||||||
| 4x-5 | - | - | - | 0 | + | + | + | |||||||
| VT | - | 0 | + | 0 | - | 0 | + |
Kết luận
VT< 0 {dấu "-"} khi x <1/3 hoắc 5/4<x<3
VT>0 {dấu "+"} khi x 1/3<5/4 hoặc x> 3
VT=0 {không có dấu} khi x={1/3;5/4;3}
c) \(h\left(x\right)=\left(x+1\right)^2+\left(\dfrac{x^2+2x+2}{x+1}\right)^2=\left(x+1\right)^2+\left(x+1+\dfrac{1}{x+1}\right)^2=2\left(x+1\right)^2+\dfrac{1}{\left(x+1\right)^2}+2\ge_{AM-GM}2\sqrt{2}+2\).
Đẳng thức xảy ra khi \(2\left(x+1\right)^2=\dfrac{1}{\left(x+1\right)^2}\Leftrightarrow x=\pm\sqrt{\dfrac{1}{2}}-1\).
b) \(g\left(x\right)=\dfrac{\left(x+2\right)\left(x+3\right)}{x}=\dfrac{x^2+5x+6}{x}=\left(x+\dfrac{6}{x}\right)+5\ge_{AM-GM}2\sqrt{6}+5\).
Đẳng thức xảy ra khi x = \(\sqrt{6}\).