Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\Leftrightarrow2x^2+4-x^2+\dfrac{3}{2}=-3+4x^2-\dfrac{4}{3}x^2+1\)
\(\Leftrightarrow x^2+\dfrac{11}{2}=\dfrac{8}{3}x^2-2\)
\(\Leftrightarrow x^2\cdot\dfrac{-5}{3}=-\dfrac{15}{2}\)
\(\Leftrightarrow x^2=\dfrac{9}{2}\)
hay \(x\in\left\{\dfrac{3\sqrt{2}}{2};-\dfrac{3\sqrt{2}}{2}\right\}\)
b: \(\Leftrightarrow\left|x\right|-4-2+\left|x\right|-\dfrac{1}{3}\left|x\right|+5=0\)
\(\Leftrightarrow\left|x\right|\cdot\dfrac{5}{3}=1\)
hay \(x\in\left\{\dfrac{3}{5};-\dfrac{3}{5}\right\}\)

3(x-2)-4(2x+1)-5(2x+3)=50
<=>(3x-6)-(8x+4)-(10x+15)=50
<=>3x-6-8x-4-10x-15=50
<=>(3x-8x-10x)+(-6-4-15)=50
<=>-15x-25=50
<=>-15x=75
<=>x=-5
\(3\frac{1}{2}:\left(4-\frac{1}{3}\left|2x+1\right|\right)=\frac{21}{22}\)
<=>\(4-\frac{1}{3}\left|2x+1\right|=\frac{7}{2}:\frac{21}{22}=\frac{11}{3}\)
<=>\(\frac{1}{3}\left|2x+1\right|=4-\frac{11}{3}=\frac{1}{3}\)
<=>\(\left|2x+1\right|=1\)
<=>2x+1=1 hoặc 2x+1=-1
<=>2x=0 hoặc 2x=-2
<=>x=0 hoặc x=-2
Vậy......................

Câu 1.
A = {15;16;17;18;19} (0,25đ)
Câu 2.
a. 2.(72 – 2.32) – 60
= 2.(49 – 2.9) – 60 (0,25đ)
= 2.31 – 60 (0,25đ)
= 62 – 60 = 2 (0,25đ)
b. 27.63 + 27.37
= 27.(63 + 37) (0,25đ)
= 27.100 (0,25đ)
= 2700 (0,25đ)
c. l-7l + (-8) + l-11l + 2
= 7 + (-8) + 11 + 2 (0,5 đ)
= 12 (0,25đ)
d. 568 – 34 {5.l9 – ( 4-1)2l + 10}
= 568 – 34 {5.[9-9] + 10} (0,25đ)
= 568 – 34.10
= 568 – 340 (0,25đ)
= 228 (0,25đ)
Câu 3.
a)2x + 3 = 52 : 5
2x + 3 =5 (0,25đ)
2x = 5-3 (0,25đ)
2x =2 (0,25đ)
x=1 (0,25đ)
b)
105 – ( x + 7) = 27 : 25
105 – ( x + 7) = 22 (0,25đ)
105 – ( x + 7) = 4 (0,25đ)
x + 7 = 105 – 4 (0,25đ)
x + 7 = 101 (0,25đ)
x = 101 – 7 (0,25đ)
x = 94 (0,25đ)
Câu 4.
Gọi x (hs) là số học sinh lớp 6B phải tìm (30<x< 38, x)
Vì hs lớp 6B xếp 2, hàng, 4 hàng, 8 hàng đều vừa đủ nên x⋮2; x⋮4; x⋮8 hay x ∈ BC{2;4;8} (0,25đ)
Ta có: BCNN(2,4,8) = 8 (0,25đ)
⇒ BC(2,4,8) = B(8) ={0; 8; 16;24; 32; 40; …}
Mặt khác: 30<x< 38 (0,25đ)
Nên x = 32
Vậy số học sinh lớp 6B là 32 học sinh (0,25đ)
Câu 5.
Khi M nằm giữa và cách đều hai điểm A và B (0,5đ)
Vẽ được hình có điểm M là trung điểm của AB (0,5đ)
Câu 6.a)

0,25đ
Điểm A nằm giữa O và B (0,25đ)
Vì OA < OB ( 4 < 8 ) (0,25đ)
Ta có: AO + AB = OB
3 + AB = 6 (0,25đ)
AB = 6 -3 = 3 cm (0,25đ)
Vậy OA = AB = 3 cm (0,25đ)
b)
Vì A nằm giữa O, B và cách đều O và B ( OA = AB ) (0,25đ)
Nên A là trung điểm OB (0,25đ)

a, Ta có: \(\left|x-\dfrac{2}{7}\right|\ge0\forall x\)
\(\Rightarrow\left|x-\dfrac{2}{7}\right|+0,5\ge0,5\forall x\)
Hay: \(A\ge0,5\forall x\)
=> Min A = 0,5 tại \(\left|x-\dfrac{2}{7}\right|=0\Rightarrow x=\dfrac{2}{7}\)
b, \(B=\left|x-5\right|+\left|x-2\right|=\left|x-5\right|+\left|2-x\right|\ge\left|x-5+2-x\right|\) =3
=> Min B = 3 tại \(\left(x-5\right)\left(2-x\right)>0\)
=)) Làm nốt
c,Tương tự b
=.= hk tốt!!

Bài 1:
a: \(\Leftrightarrow x\cdot\dfrac{3}{4}=-1\)
hay x=-4/3
b: =>x=4/8+3/7=1/2+3/7=7/14+6/14=13/14
Bài 3:
BCNN(16;32;5)=160
UCLN(16;32;5)=1

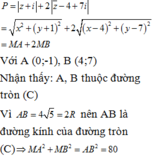

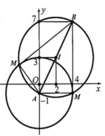
a. 1,7
b.3/7