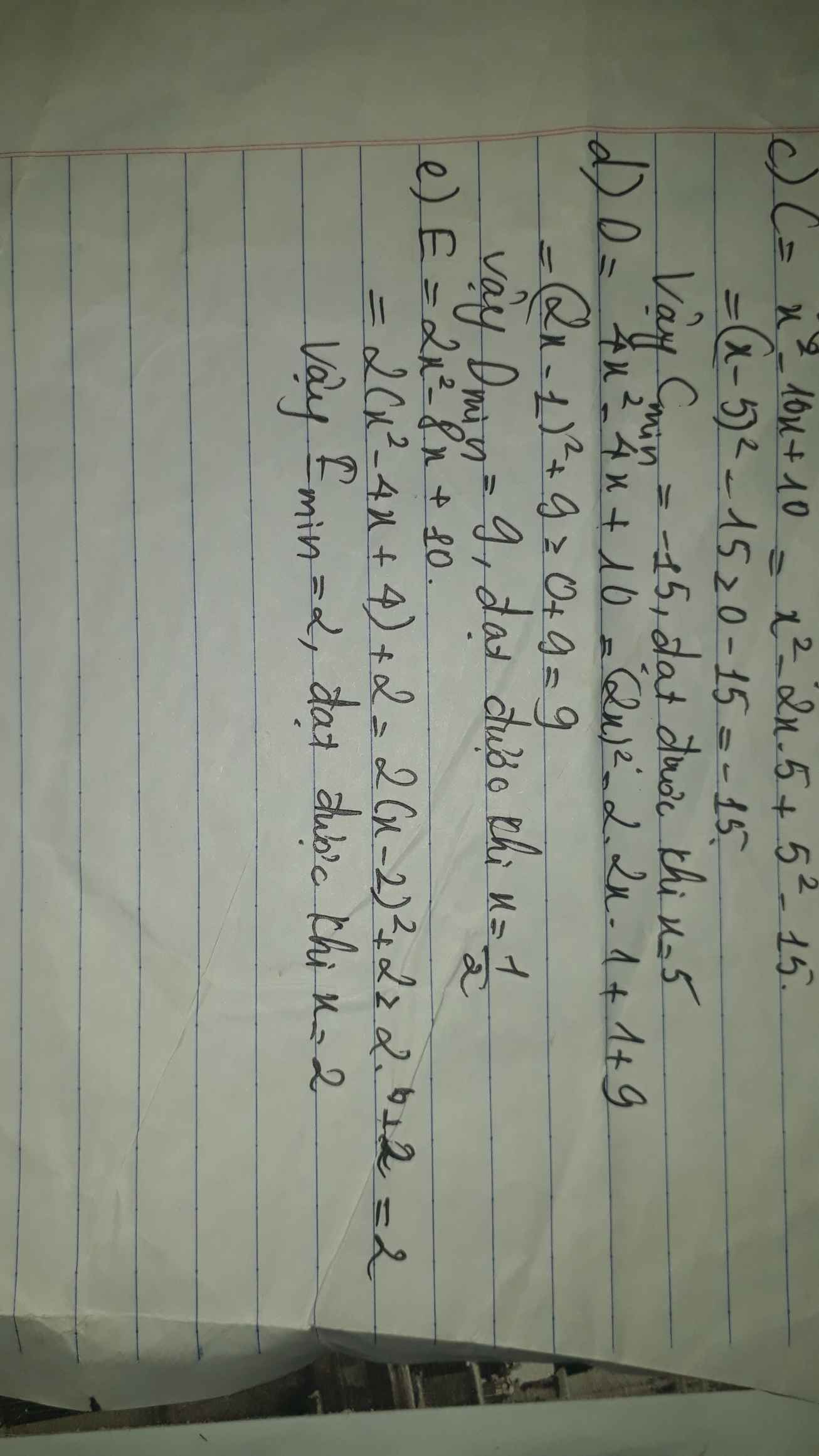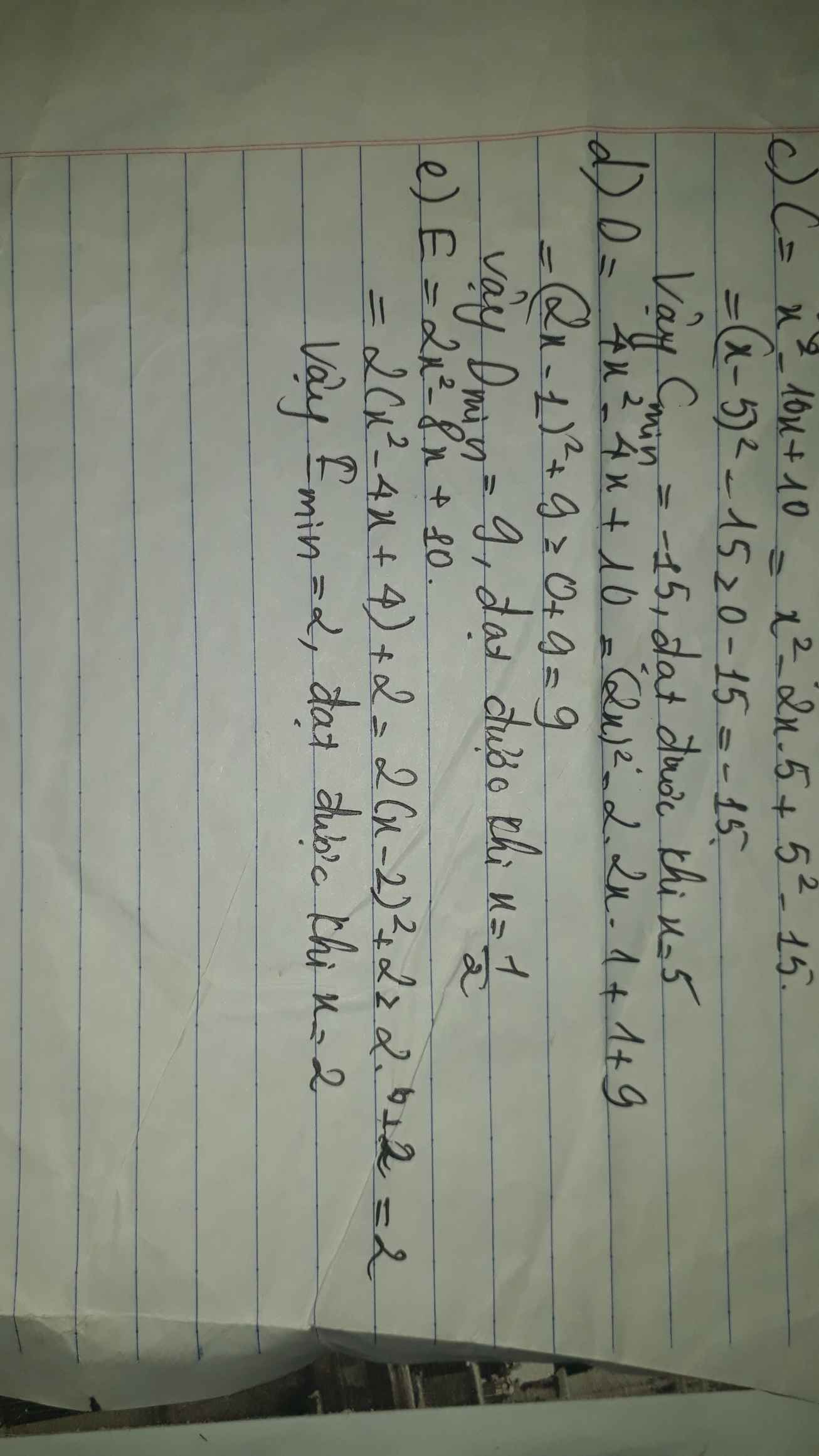
Tìm GTNN của a) A= $x^2+4x+10$b) B= $x^2-2x+10$c) C= \(x^2-...

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Đàm Tùng Vận

30 tháng 7 2021

Tìm GTNN của

a) A= $x^2+4x+10$

b) B= $x^2-2x+10$

c) C= $x^2-10x+10$

d) D= $4x^2-4x+10$

e) E= $2x^2-8x+10$

Giup mk vs ai làm nhanh mk sẽ vote cho bạn đó

#Toán lớp 8

Trên con đường thành công không có....

30 tháng 7 2021

undefined

Đúng(1)

Trên con đường thành công không có....

30 tháng 7 2021

undefined

Đúng(1)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Vân Anh

4 tháng 5 2016 - olm

Câu 1: TIìm GTLN, GTNN của:a) $B=\frac{4x^2+2x+1}{4x^2+1}$b)$E=\frac{3x^2-8x+13}{x^2+1}$c)$D=\frac{8x+3}{4x^2+1}$ d)$C=\frac{4x+1}{4x^2+2}$e)$A=\frac{2x+1}{x^2+2}$Câu 2: Tìm GTLN của:a) $A=\frac{x^2+10}{2x^2+3}$b)$B=\frac{3y^2-6y+27}{2y^2-4y+10}$Câu 3: Tìm GTNN...

Đọc tiếp

#Toán lớp 8

Dương Thùy

19 tháng 7 2018

Tìm GTNN của các biểu thức sau: A= 11-10x-x2 B= 6x-x2-5 C= 2x-2x2-5 D= (2-x). (x+4) E= -x2-4x+2 F= 4x-x2+3 G= x2-6x+11 H= 2x2+10x-1 P= 5x+x2 Q= 5x2-8x-10 I= 9x+3x2 ...

Đọc tiếp

#Toán lớp 8

Nguyễn Lê Phước Thịnh

28 tháng 7 2022

a: $=-\left(x^2+10x-11\right)$

$=-\left(x^2+10x+25-36\right)$

$=-\left(x+5\right)^2+36< =36$

Dấu '=' xảy ra khi x=-5

b: $=-\left(x^2-6x+5\right)$

$=-\left(x^2-6x+9-4\right)$

$=-\left(x-3\right)^2+4< =4$

Dấu '=' xảy ra khi x=3

c: $=-2\left(x^2-x+\dfrac{5}{2}\right)$

$=-2\left(x^2-x+\dfrac{1}{4}+\dfrac{9}{4}\right)$

$=-2\left(x-\dfrac{1}{2}\right)^2-\dfrac{9}{2}< =-\dfrac{9}{2}$

Dấu '=' xảy ra khi x=1/2

d: $=2x+8-x^2-4x$

$=-x^2-2x+8$

$=-\left(x^2+2x-8\right)$

$=-\left(x^2+2x+1-9\right)$

$=-\left(x+1\right)^2+9< =9$

Dấu '=' xảy ra khi x=-1

Đúng(0)

ღHàn Thiên Băng ღ

3 tháng 12 2018 - olm

Tìm GTNN; GTLN của các biểu thức sau:

a) A= x²- 4x + 1

b) B= 5 - 8x - x²

c) C= 5x - x²

d) D= ( x - 1 )(x + 3)( x + 2 )( x + 6)

$E=\frac{1}{x^2+5x+14}$

f)$F=\frac{2x^2+4x+10}{x^2+2x+3}$

#Toán lớp 8

luuthianhhuyen

3 tháng 12 2018

$x^2-4x+1=x^2-2\cdot x\cdot2+4-4+1=\left(x-2\right)^2-4+1$

$=\left(x-2\right)^2-3$ $\forall x\in Z$

$\Rightarrow A_{min}=-3khix=2$

Đúng(0)

Nguyệt

3 tháng 12 2018

$a,A=x^2-4x+1=x^2-2.2.x+2^2-3=\left(x-2\right)^2-3\ge-3$

dấu = xảy ra khi x-2=0

=> x=2

Vậy MinA=-3 khi x=2

$b,B=5-8x-x^2=-\left(x^2+8x+5\right)=-\left(x^2+2.4.x+4^2\right)+9=-\left(x+4\right)^2+9\le9$

dấu = xảy ra khi x+4=0

=> x=-4

Vậy MaxB=9 khi x=-4

$c,C=5x-x^2=-\left(x^2-5x\right)=-\left(x^2-\frac{2.x.5}{2}+\frac{25}{4}\right)+\frac{25}{4}=-\left(x-\frac{5}{2}\right)^2+\frac{25}{4}\le\frac{25}{4}$

dấu = xảy ra khi $x-\frac{5}{2}=0$

=> x=$\frac{5}{2}$

Vậy Max C=$\frac{25}{4}$khi x=$\frac{5}{2}$

$E=\frac{1}{x^2+5x+14}=\frac{1}{x^2+\frac{2.x.5}{2}+\frac{25}{4}+\frac{31}{4}}=\frac{1}{\left(x+\frac{5}{2}\right)^2+\frac{31}{4}}$

$\left(x+\frac{5}{2}\right)^2+\frac{31}{4}\ge\frac{31}{4}$

dấu = xảy ra khi $x+\frac{5}{2}=0$

=> x$=-\frac{5}{2}$

vì tử thức >0,mẫu thức nhỏ nhất và lớn hơn 0 => E lớnnhất khi mẫu thức nhỏ nhất

Vậy $MaxE=\frac{31}{4}$khi x$=-\frac{5}{2}$

Đúng(0)

Yuki Nguyễn

3 tháng 12 2018

Tìm GTNN; GTLN của các biểu thức sau:

a) A= x²- 4x + 1

b) B= 5 - 8x - x²

c) C= 5x - x²

d) D= ( x - 1 )(x + 3)( x + 2 )( x + 6)

e) $E=\dfrac{1}{x^2+5x+14}$

f)$F=\dfrac{2x^2+4x+10}{x^2+2x+3}$

#Toán lớp 8

Akai Haruma

Giáo viên

26 tháng 12 2018

Câu a:
$A=x^2-4x+1=(x^2-4x+4)-3$

$=(x-2)^2-3\geq 0-3=-3$

Dấu "=" xảy ra khi $(x-2)^2=0$ hay $x=2$

Vậy GTNN của $A$ là $-3$ khi $x=2$

Câu b:

$B=5-8x-x^2=21-(x^2+8x+16)$

$=21-(x+4)^2\leq 21-0=21$

Dấu "=" xảy ra khi $(x+4)^2=0$ hay $x=-4$

Vậy GTLN của $B$ là $21$ khi $x=-4$

Đúng(0)

Akai Haruma

Giáo viên

26 tháng 12 2018

Câu c:

$C=5x-x^2=-(x^2-5x)=\frac{25}{4}-(x^2-5x+\frac{5^2}{2^2})$

$=\frac{25}{4}-(x-\frac{5}{2})^2\leq \frac{25}{4}-0=\frac{25}{4}$

Dấu "=" xảy ra khi $(x-\frac{5}{2})^2=0\Leftrightarrow x=\frac{5}{2}$

Vậy GTLN của $C$ là $\frac{25}{4}$ khi $x=\frac{5}{2}$

Câu d:

$D=(x-1)(x+3)(x+2)(x+6)=[(x-1)(x+6)][(x+3)(x+2)]$

$=(x^2+5x-6)(x^2+5x+6)$

$=(x^2+5x)^2-6^2=(x^2+5x)^2-36\geq 0-36=-36$

Dấu "=" xảy ra khi $(x^2+5x)^2=0\Leftrightarrow \left[\begin{matrix} x=0\\ x=-5\end{matrix}\right.$

Vậy GTNN của $D$ là $-36$ khi $x=0$ hoặc $x=-5$

Đúng(0)

ko biet

30 tháng 7 2018 - olm

Tìm GTLN của:

a, A=-x²+6x-10

b,B=-2x²-4x-10

c,-2x²+3x-10

d,-x²-y²+2x-4y-10

e,-x²-3y²-2xy-2x+2y-10

#Toán lớp 8

phạm thị hồng nhung

30 tháng 7 2018

a) A= -x² + 6x -10

= -(x² - 6x) -10

= -(x² - 2. x .3 +3² -9)- 10

= -( x-3 )² +9 -10

= - (x-3)² -1 $\le$-1 với mọi giá trị của x

Dấu '' = '' xảy ra khi và chỉ khi

x-3 =0

$\Leftrightarrow$x=3

Vậy giá trị lớn nhất của biểu thức A là -1 tại x =3

CÁC PHẦN KHÁC CẬU LÀM TƯƠNG TỰ

b) B= -2x²-4x-10

= -2(x²+ 2x ) -10

= -2 (x² +2x+1² -1)-10

=-2(x+1)² +2 -10

=-2(x+1)² -8 $\le$-8 với mọi giá trị của x

Dấu " ='' xảy ra khi và chỉ khi

x+1=0

............................

c) C= -2x² +3x -10

= -2(x² -$\frac{3}{2}$x) -10

= -2( x² - 2.x.$\frac{3}{4}$+ $\frac{3^2}{4^2}$-$\frac{9}{16}$)-10

= -2(x-$\frac{3}{4}$)²+$\frac{9}{8}$-10

=-2(x- $\frac{3}{4}$)² +$\frac{-71}{8}$$\le$$\frac{-71}{8}$với mọi giá trị của x

Dấu bằng ''='' xảy ra khi và chi khi

x-$\frac{3}{4}$=0

.......................................................

d) D= -x² -y²+2x-4y -10

=(-x²+2x) +( -y² -4y) -10

= -(x² -2x+1 -1) -(y² +4y+2²-4 )-10

=-(x-1)² +1 -(y+2)² +4 -10

=-(x-1)² - (y+2)² -5 $\le$5 với mọi giá tri của x

Dấu '' ='' xảy ra khi và chỉ khi

$\hept{\begin{cases}x-1=0\\y+2=0\end{cases}}$

......................................................

e) XIN LỖI TỚ CHƯA NGHĨ RA

Đúng(0)

Ngọc Hà Nguyễn

23 tháng 6 2019 - olm

Tìm GTNN:
a, A= 6x² -6x +1
b,B= 3+ 2x+ 3x²

c,C= 4x+ 2x²- 3

d,D= 10x+ 6+ x²

e,E= 8x²- 6x +3

#Toán lớp 8

Edogawa Conan

23 tháng 6 2019

a) Ta có:A = 6x² - 6x + 1 = 6(x² - x + 1/4) - 1/2 = 6(x - 1/2)² - 1/2

Ta luôn có : (x - 1/2)² $\ge$0 $\forall$x --> 6(x - 1/2)² $\ge$ 0 x

=> 6(x - 1/2)² - 1/2 $\ge$-1/2 $\forall$x

hay A $\ge$-1/2 $\forall$x

Dấu "=" xảy ra khi : (x - 1/2)² = 0 <=> x - 1/2 = 0 <=> x = 1/2

Vậy A_min = -1/2 tại x = 1/2

Đúng(0)

Phạm Thị Thùy Linh

23 tháng 6 2019

$a,A=6x^2-6x+1$

$=6\left(x^2-x+\frac{1}{6}\right)$

$=6\left[\left(x^2-2.x.\frac{1}{2}+\frac{1}{4}\right)-\frac{1}{4}+\frac{1}{6}\right]$

$=6\left[\left(x-\frac{1}{2}\right)^2-\frac{1}{12}\right]$

$=6\left(x-\frac{1}{2}\right)^2-\frac{1}{2}$

$A_{min}=-\frac{1}{12}\Leftrightarrow\left(x-\frac{1}{2}\right)^2=0$

$\Rightarrow x-\frac{1}{2}=0\Rightarrow x=\frac{1}{2}$

Đúng(0)

Nguyễn Ngọc Hà

23 tháng 6 2019

Tìm GTNN:
a, A= 6x² -6x +1
b,B= 3+ 2x+ 3x²

c,C= 4x+ 2x²- 3

d,D= 10x+ 6+ x²

e,E= 8x²- 6x +3

#Toán lớp 8

lê thị hương giang

23 tháng 6 2019

$a,A=6x^2-6x+1$

$=6\left(x^2-x+\frac{1}{4}\right)-\frac{1}{2}$

$=6\left(x-\frac{1}{2}\right)^2-\frac{1}{2}\ge-\frac{1}{2}$

Dấu = xảy ra $\Leftrightarrow x=\frac{1}{2}$

Vậy $Min_A=-\frac{1}{2}\Leftrightarrow x=\frac{1}{2}$

$b,B=3+2x+3x^2$

$=3\left(x^2+\frac{2}{3}x+\frac{1}{9}\right)+\frac{8}{3}$

$=3\left(x+\frac{1}{3}\right)^2+\frac{8}{3}\ge\frac{8}{3}$

Dấu = xảy ra $\Leftrightarrow x=-\frac{1}{3}$

Vậy $Min_B=\frac{8}{3}\Leftrightarrow x=-\frac{1}{3}$

$c,C=4x+2x^2-3$

$=2\left(x^2+2x+1\right)-5$

$=2\left(x+1\right)^2-5\ge-5$

Dấu = xảy ra $\Leftrightarrow x=-1$

Vậy $Min_C=-5\Leftrightarrow x=-1$

$d,D=10x+6+x^2$

$=\left(x^2+10x+25\right)-19$

$=\left(x+5\right)^2-19\ge-19$

Dấu = xảy ra $\Leftrightarrow x=-5$

Vậy $Min_D=-19\Leftrightarrow x=-5$

$e,E=8x^2-6x+3$

$=8\left(x^2-\frac{3}{4}x+\frac{9}{64}\right)+\frac{15}{8}$

$=8\left(x-\frac{3}{8}\right)^2+\frac{15}{8}\ge\frac{15}{8}$

Dấu = xảy ra $\Leftrightarrow x=\frac{3}{8}$

Vậy $Min_E=\frac{15}{8}\Leftrightarrow x=\frac{3}{8}$

Đúng(0)

Trương Tuấn Hưng

13 tháng 4 2020

giai pt (giup toi voi)

1.$\dfrac{4x}{4x^2-8x+7}+\dfrac{3x}{4x^2-10x+7}=1$

2.$\dfrac{2x}{x^2+3x-10}$+$\dfrac{5x}{x^2+7x-10}=4$

#Toán lớp 8

Nguyễn Việt Lâm

Giáo viên

13 tháng 4 2020

Hai câu là hoàn toàn giống nhau, mình làm câu a, câu b bạn tự làm tương tự:

ĐKXĐ: ...

Nhận thấy $x=0$ ko phải nghiệm, pt tương đương:

$\frac{4}{4x+\frac{7}{x}-8}+\frac{3}{4x+\frac{7}{x}-10}=1$

Đặt $4x+\frac{7}{x}-10=t$

$\Leftrightarrow\frac{4}{t+2}+\frac{3}{t}=1\Leftrightarrow4t+3\left(t+2\right)=t\left(t+2\right)$

$\Leftrightarrow t^2-5t-6=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=6\end{matrix}\right.$

$\Rightarrow\left[{}\begin{matrix}4x+\frac{7}{x}-10=-1\\4x+\frac{7}{x}-10=6\end{matrix}\right.$

$\Leftrightarrow\left[{}\begin{matrix}4x^2-9x+7=0\\4x^2-16x+7=0\end{matrix}\right.$ (bấm casio)

Đúng(0)

Trương Tuấn Hưng

13 tháng 4 2020

cảm ơn

Đúng(0)

Hồ Quang Phước

2 tháng 1 2018

tim gia tri cua x de bieu thuc

A=$\dfrac{-4}{x^2-4x+10}$ co GTNN

B= -2 + 4x +1 co GTLN

C= $\dfrac{2}{x^2+4x+5}$ co GTLN

D= $\dfrac{5}{x^2-6x+12}$ co GTLN

E=$\dfrac{x^2-2x+2018}{x^2}$ co GTNN

#Toán lớp 8

Ngô Tấn Đạt

2 tháng 1 2018

$A=-\dfrac{4}{x^2-4x+10}\\ =-\dfrac{4}{\left(x^2-2.x.2+4+6\right)}\\ =-\dfrac{4}{\left(x-2\right)^2+6}$

$\left(x-2\right)^2\ge0\\ \Rightarrow\left(x-2\right)^2+6\ge6\\ \Rightarrow\dfrac{4}{\left(x-2\right)^2+6}\le\dfrac{2}{3}\\ \Rightarrow A=-\dfrac{4}{\left(x-2\right)^2+6}\ge-\dfrac{2}{3}$

Min A=-2/3 khi x=2

Đúng(0)

Nguyễn Thị Ngọc Thơ

3 tháng 1 2018

$C=\dfrac{2}{x^2+4x+5}=\dfrac{2}{\left(x+2\right)^2+1}$

Vì $\left(x+2\right)^2\ge0\Rightarrow\left(x+2\right)^2+1\ge1$

$\Rightarrow C\le2$

Dấu ''='' xảy ra $\Leftrightarrow x=-2$

Vậy Min C = 2 kjhi x = -2

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP