
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=\dfrac{x^2+x+5}{\left(x+1\right)^2}\)
Đặt \(x+1=t\Rightarrow x=t-1\)
\(\Rightarrow A=\dfrac{\left(t-1\right)^2+t-1+5}{t^2}=\dfrac{t^2-t+5}{t^2}=\dfrac{5}{t^2}-\dfrac{1}{t}+1=5\left(\dfrac{1}{t}-\dfrac{1}{10}\right)^2+\dfrac{19}{20}\ge\dfrac{19}{20}\)
\(A_{min}=\dfrac{19}{20}\) khi \(t=10\) hay \(x=9\)

a) Ta có: \(M=-x^2-4x+20\)
\(=-\left(x^2+4x-20\right)\)
\(=-\left(x^2+4x+4-24\right)\)
\(=-\left(x+2\right)^2+24\le24\forall x\)
Dấu '=' xảy ra khi x=-2




\(A=\left(x^2-2xy+y^2\right)+\left(y^2-2yz+z^2\right)+\left(z^2-2xz+x^2\right)+\left(x^2+2x+1\right)+1\\ A=\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2+\left(x+1\right)^2+1\ge1\\ A_{min}=1\Leftrightarrow x=y=z=-1\)

\(A=\)\(x^2+y^2-4x+y+5.\)
\(=\left(x^2-4x+4\right)+\left(y^2+2.y.\frac{1}{2}+\frac{1}{4}\right)+\frac{3}{4}\)
\(=\left(x-2\right)^2+\left(y+\frac{1}{2}\right)^2+\frac{3}{4}\)
\(\Rightarrow A_{min}=\frac{3}{4}\Leftrightarrow\)\(\hept{\begin{cases}\left(x-2\right)^2=0\\\left(y+\frac{1}{2}\right)^2=0\end{cases}\Rightarrow\hept{\begin{cases}x=2\\y=-\frac{1}{2}\end{cases}}}\)
\(x^2+y^2-4x+y+5=\left(x-2\right)^2+\left(y+\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
\(\Rightarrow Min=\frac{3}{4}\)Dấu "=" xr \(\Leftrightarrow\hept{\begin{cases}x-2=0\\y+\frac{1}{2}=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=2\\y=-\frac{1}{2}\end{cases}}}\)

Câu này em đã hỏi rồi
1.Tìm GTNN của Bthức : B= 4x2- 6x+1 : (x-2)2 với x ≠ 22. Tìm GTLN của Bthức: C= x2 + 4x - 14 : x2 -2x +1 với x≠ 1gi... - Hoc24

Bài làm:
Ta có: \(5\left(m-3\right)^2-5\)
\(\ge-5\left(\forall m\right)\)
Dấu "=" xảy ra khi: \(\left(m-3\right)^2=0\Rightarrow m=3\)
Vậy \(Min=-5\Leftrightarrow m=3\)
\(5\left(m-3\right)^2-5\)
Ta có : \(5\left(m-3\right)^2\ge0\forall m\Rightarrow5\left(m-3\right)^2-5\ge-5\)
Dấu " = " xảy ra <=> m - 3 = 0 => m = 3
Vậy GTNN của biểu thức = -5, đạt được khi m = 3

Lời giải:
$D=(x+1)(x^2-4)(x+5)+2014$
$=(x+1)(x+2)(x-2)(x+5)+2014$
$=(x^2+3x+2)(x^2+3x-10)+2014$
$=t(t-12)+2014$ (đặt $x^2+3x+2=t$)
$=t^2-12t+2014=(t-6)^2+1978$
$=(x^2+3x-4)^2+1978\geq 1978$
Vậy gtnn của biểu thức là $1978$. Giá trị này đạt tại $x^2+3x-4=0$
$\Leftrightarrow x=1$ hoặc $x=-4$
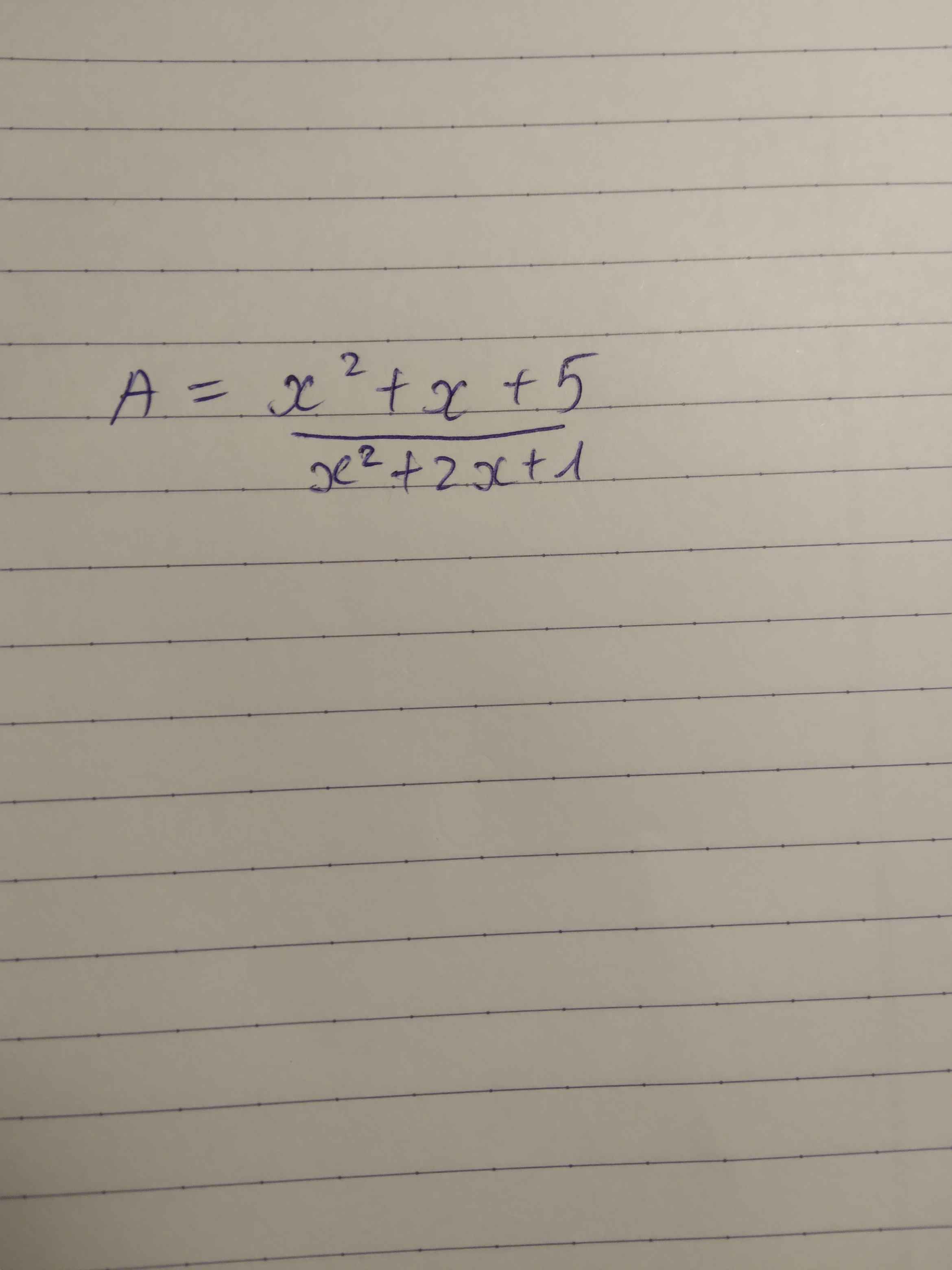

Ta có : \(\left(3x+2\right)^2+3\ge3\forall x\)
\(\Rightarrow\frac{6}{\left(3x+2\right)^2+3}\le\frac{6}{3}=2\)
\(\Rightarrow C=\frac{-6}{\left(3x+2\right)^2+3}\ge-2\)
Dấu "=" xảy ra \(\Leftrightarrow3x+2=0\) \(\Leftrightarrow x=-\frac{2}{3}\)