PK
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
ND
1
8 tháng 9 2019
a) \(\sqrt{x^2-10+25}\)=lx-5l=2
=>x=7 hoặc x=3
b) bình phường lên ta đc x^2-2x=25
từ đây bạn giải bình thường là đc chúc hk tốt
NH
25 tháng 3 2017
a)\(\sqrt{3x^2+6x+7}+\sqrt{5x^2+10x+21}\)
=\(\sqrt{3\left(x+1\right)^2+4}+\sqrt{5\left(x+1\right)^2+16}\ge6\)(1)
mặt khác 5-2x-x2=6-(x+1)2\(\le6\)(2)
từ (1) và (2)=>dấu = xảy ra khi VP =6 =VTtức x=-1
b)\(\sqrt{3x^2+6x+12}\)+\(\sqrt{5x^4+10x^2+9}\)
=\(\sqrt{3\left(x+1\right)^2+9}+\sqrt{5\left(x^2+1\right)^2+4}>5\)(x2+1>0)(1')
mặt khác VP=5-2(x+1)2\(\le\)5(2')
từ (1') và (2')=> pt vô nghiệm
SL
3
H
27 tháng 8 2023
ĐK: \(x>0\)
PT trở thành:
\(x+2=3\sqrt{x}\\ \Leftrightarrow x-3\sqrt{x}+2=0\\ \Leftrightarrow x-2\sqrt{x}-\sqrt{x}+2=0\\ \Leftrightarrow\sqrt{x}\left(\sqrt{x}-2\right)-\left(\sqrt{x}-2\right)=0\\ \Leftrightarrow\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x}-2=0\\\sqrt{x}-1=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\x=1\left(tm\right)\end{matrix}\right.\)
Vậy PT có nghiệm `x=4` hoặc `x=1`
T
27 tháng 8 2023
\(\dfrac{x+2}{\sqrt{x}}=3\) (ĐKXĐ: x > 0)
\(\Leftrightarrow x+2=3\sqrt{x}\)
\(\Leftrightarrow x-3\sqrt{x} +2=0\)
\(\Leftrightarrow x-\sqrt{x}-2\sqrt{x}+2=0\)
\(\Leftrightarrow\sqrt{x}\left(\sqrt{x}-1\right)-2\left(\sqrt{x}-1\right)=0\)
\(\Leftrightarrow\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}-2=0\\\sqrt{x}-1=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=1\end{matrix}\right.\) (tm)
#Ayumu
29 tháng 8 2021
\(a,ĐK:x\in R\)
\(b,ĐK:\dfrac{-7}{8-10x}\ge0\Leftrightarrow8-10x< 0\left(-7< 0\right)\Leftrightarrow x>\dfrac{4}{5}\)
\(c,ĐK:\dfrac{24-6x}{-7}\ge0\Leftrightarrow24-6x\le0\left(-7< 0\right)\Leftrightarrow x\ge4\)
H9
HT.Phong (9A5)
CTVHS
8 tháng 8 2023
Ta có: \(P=\dfrac{\sqrt{a}+3}{\sqrt{a}-2}-\dfrac{\sqrt{a}-1}{\sqrt{a}+2}+\dfrac{4\sqrt{a}}{4-\sqrt{a}}\)
a) ĐKXĐ: \(a\ne4;a\ne16;a\ge0\)
\(P=\dfrac{\sqrt{a}+3}{\sqrt{a}-2}-\dfrac{\sqrt{a}-1}{\sqrt{a}+2}-\dfrac{4\sqrt{a}}{\sqrt{a}-4}\)
\(P=\dfrac{\left(\sqrt{a}+3\right)\left(\sqrt{a}+2\right)}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}-\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}-\dfrac{4\sqrt{a}}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}\)
\(P=\dfrac{a+3\sqrt{a}+2\sqrt{a}+6-a+2\sqrt{a}+\sqrt{a}-2-4\sqrt{a}}{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}\)
\(P=\dfrac{4\sqrt{a}+4}{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}\)
\(P=\dfrac{4\sqrt{a}+4}{a-4}\)
b) Thay x=9 vào P ta có:
\(P=\dfrac{4\cdot\sqrt{9}+4}{9-4}=\dfrac{16}{5}\)
c) \(P< 0\) khi:
\(\dfrac{4\sqrt{x}+4}{a-4}< 0\)
Mà: \(4\sqrt{x}+4>0\)
\(\Rightarrow a-4< 0\)
\(\Rightarrow a< 4\)
kết hợp với Đk ta có:
\(0\le x< 4\)
31 tháng 5 2016
a)Ta có : \(\sqrt{x}=x\left(DK:x\ge0\right)\)
\(\Leftrightarrow x=x^2\Leftrightarrow x^2-x=0\Leftrightarrow x\left(x-1\right)=0\Rightarrow x=0\)(nhận ) hoặc \(x=1\)(Nhận)
Vậy tập nghiệm của phương trình là : \(S=\left\{0;1\right\}\)
b) \(\sqrt{x^2+x+1}=x+2\left(DK:x\ge-2\right)\)
\(\Leftrightarrow x^2+x+1=\left(x+2\right)^2\)\(\Leftrightarrow x^2+x+1=x^2+4x+4\Leftrightarrow3x=-3\Leftrightarrow x=-1\)( Nhận)
Vậy tập nghiệm của phương trình là : \(S=\left\{-1\right\}\)
c) \(\sqrt{x^2-10x+25}=x-3\left(DK:x\ge3\right)\)
\(\Leftrightarrow\sqrt{\left(x-5\right)^2}=x-3\Leftrightarrow\left|x-5\right|=x-3\)(1)
Đến đây ta xét hai trường hợp :
1. Với \(3\le x< 5\)phương trình (1) tương đương với :
\(5-x=x-3\Leftrightarrow2x=8\Leftrightarrow x=4\)(Nhận)
2. Với \(x\ge5\)phương trình (1) tương đương với :
\(x-5=x-3\Rightarrow-5=-3\)( vô lí )
Vậy tập nghiệm của phương trình là : \(S=\left\{4\right\}\)
c) \(\sqrt{x-2}+\sqrt{2-x}=0\)
Ta có điều kiện xác định của phương trình là : \(\hept{\begin{cases}x-2\ge0\\2-x\ge0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ge2\\x\le2\end{cases}\Rightarrow}x=2}\)
Thử lại với x = 2 ta thấy thoả mãn nghiệm của phương trình.
Vậy tập nghiệm của phương trình là : \(S=\left\{2\right\}\)
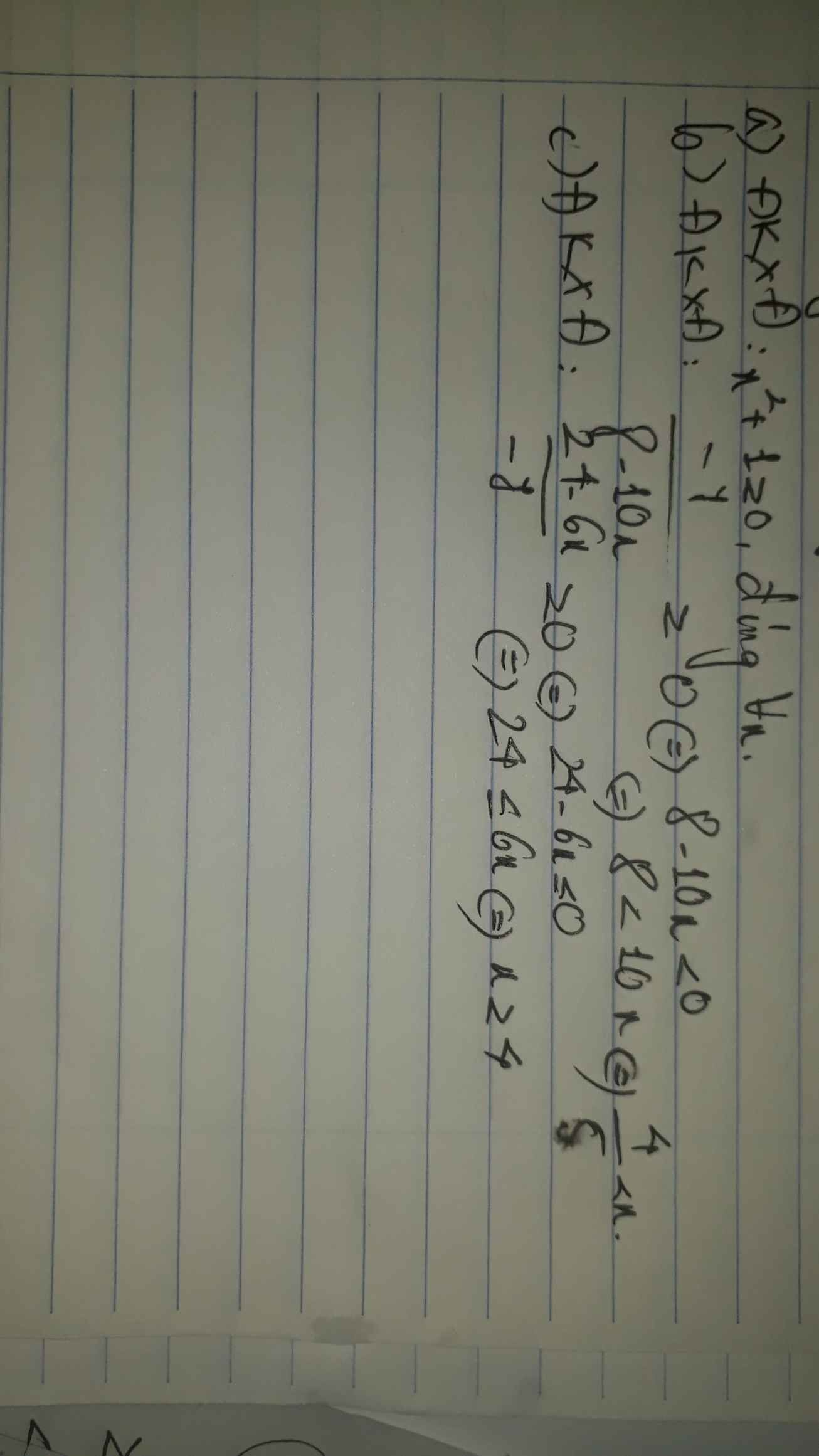
Bmin=5 xay ra dau= khi va chi khi x=5
\(B=\sqrt{x^2-10x+34}+\sqrt{x^2-10x+29}\)
\(=\sqrt{\left(x-5\right)^2+9}+\sqrt{\left(x-5\right)^2+4}\)\(\ge\)\(\sqrt{9}+\sqrt{4}=5\)
Vậy Min \(B=5\)khi \(x=5\)