K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
2
IM
5 tháng 11 2016
Ta có :
\(x^2+2x+5=x^2+2x+1+4=\left(x+1\right)^2+4\)
\(\Rightarrow B=\frac{3}{\left(x+1\right)^2+4}\)
Vì \(\left(x+1\right)^2\ge0\forall x\)
\(\Rightarrow\left(x+1\right)^2+4\ge4\)
\(\Rightarrow\frac{3}{\left(x+1\right)^2+4}\le\frac{3}{4}\)
\(\Rightarrow B\le\frac{3}{4}\)
Dấu " = " xảy ra khi x = - 1
Vậy MAXB= 3 / 4 khi x = - 1
NH
1
31 tháng 5 2023
A=3(x^2+2/3x-1)
=3(x^2+2*x*1/3+1/9-10/9)
=3(x+1/3)^2-10/3>=-10/3
Dấu = xảy ra khi x=-1/3
\(B=1+\dfrac{15}{x^2+x+5}=1+\dfrac{15}{\left(x+\dfrac{1}{2}\right)^2+\dfrac{19}{4}}< =1+15:\dfrac{19}{4}=1+\dfrac{60}{19}=\dfrac{79}{19}\)
Dấu = xảy ra khi x=-1/2
LM
26 tháng 8 2016
a/ A = x2 + (y - 1)4 - 3
Do x2\(\ge\) 0 và (y - 1)4\(\ge\)0
=> A = x2 + (y - 1)4 - 3 \(\ge\)-3
Đẳng thức xảy ra khi: x = 0 và y - 1 = 0 => x = 0 và y = 1
Vậy GTNN của A là -3 khi x = 0 và y = 1
b/ B = 3(x2 - 7) + 2016 = 3x2 - 21 + 2016 = 3x2 + 1995
Mà: 3x2\(\ge\)0 => B = 3x2 + 1995 \(\ge\)1995
Đẳng thức xảy ra khi: 3x2 = 0 => x = 0
Vậy GTNN của B là 1995 khi x = 0
c/ C = (2x + 3)(x - 5) - x(x - 7) = 2x2 - 10x + 3x -15 - (x2 - 7x) = 2x2 - 7x -15 - x2 + 7x = (2x2 -x2) + (-7x + 7x) - 15 = x2 -15
Mà: x2\(\ge\)0 => x2 - 15\(\ge\)-15
Đẳng thức xảy ra khi: x2 = 0 => x = 0
Vậy GTNN cảu C là -15 khi x = 0
NN
3 tháng 7 2020
Đặt \(A=-x^2-2x+3\)
\(\Rightarrow A=-x^2-2x-1+4=-\left(x^2+2x+1\right)+4=-\left(x+1\right)^2+4\)
Vì \(\left(x+1\right)^2\ge0\forall x\)
\(\Rightarrow-\left(x+1\right)^2\le0\forall x\)
\(\Rightarrow-\left(x+1\right)^2+4\le4\forall x\)
hay \(A\le4\)
Dấu " = " xảy ra \(\Leftrightarrow x+1=0\)\(\Leftrightarrow x=-1\)
Vậy \(maxA=4\)\(\Leftrightarrow x=-1\)
3 tháng 7 2020
-x2 - 2x + 3
<=> -x2 - 2x - 1 + 4
<=> -( x2 + 2x + 1 ) + 4
<=> -( x + 1 )2 + 4
\(\left(x+1\right)^2\ge\forall x\Rightarrow-\left(x+1\right)^2\le0\forall x\)
\(\Rightarrow-\left(x+1\right)^2+4\le4\forall x\)
Dấu = xảy ra <=> x + 1 = 0
<=> x = -1
Vậy GTLN của đa thức = 4 khi x = -1
TN
16 tháng 6 2016
Vì bài dài nên mk làm hơi tắt tí nhé có chỗ nào ko hiểu thì nhắn lại với mình :))
1) Ta thấy:\(5+\left|x-2\right|\le5+0=5\)\(B=8-\left|x+3\right|\le8-0=8\)
Vậy MaxA=5<=>x=2
2) Ta thấy:\(B=8-\left|x+3\right|\le8-0=8\)
Vậy MaxB=8<=>x=-3
3) Ta thấy:\(2\left|x-3\right|+5\ge0+5=5\)
Vậy MinC=5<=>x=3
4)Ta thấy:\(6-3\left|2x-1\right|\le6-0=6\)
Vậy MaxD=6<=>x=1/2
5)mấy câu 5,6,7 bạn dùng BĐT |a|+|b|>=|a+b| nhé
\(E=\left|x-2\right|+\left|5-x\right|\ge\left|x-2+5-x\right|=7\)
Vậy MinE=7<=>x=2 hoặc 5
6)\(F=\left|7-x\right|+\left|x+1\right|\ge\left|7-x+x+1\right|=8\)
Vậy MinF=8<=>x=7 hoặc -1
7)\(H=\left|x+3\right|+\left|x-2\right|\ge\left|x+3-x-2\right|=1\)
Vậy MinH=1<=>x=-3 hoặc 2
8) I=|7-1|+|-2-1|
I=9 (đề bắt tìm Min và Max sao câu này ko có x nhỉ )
SS
1
VD
28 tháng 8 2018
-Ta có: \(--5-\left(y-5\right)^2-\left|2x-3\right|\le-5\)
Dấu "=" xảy ra khi: \(\hept{\begin{cases}y=5\\x=\frac{3}{2}\end{cases}}\)
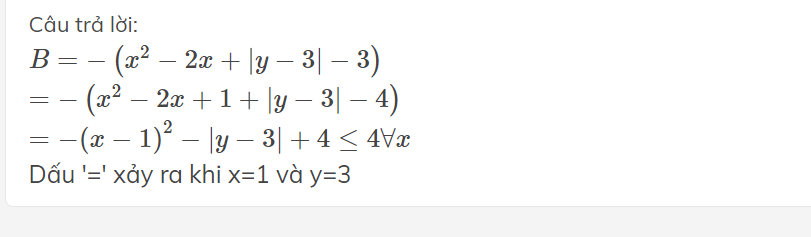
\(B=\frac{3}{x^2+2x+5}=\frac{3}{x^2+2x+4+1}\)
\(=\frac{3}{\left(x+2\right)^2+1}\le\frac{3}{1}=3\)
\(\Rightarrow B\le3\)
Dấu = khi (x+2)2=0 <=>x+2=0 <=>x=-2
Vậy MaxB=3 khi x=-2