
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ : \(x>0\)
Áp dụng bất đẳng thức Cauchy cho 2 số dương \(\sqrt{x};\dfrac{4}{\sqrt{x}}\) ta có
\(P=\sqrt{x}+\dfrac{4}{\sqrt{x}}\ge2\sqrt{\sqrt{x}.\dfrac{4}{\sqrt{x}}}=4\)
Dấu "=" xảy ra khi \(\sqrt{x}=\dfrac{4}{\sqrt{x}}\Leftrightarrow x=4\)
\(P=\sqrt[]{x}+\dfrac{4}{\sqrt[]{x}}\left(x>0\right)\)
\(P=\dfrac{x+4}{\sqrt[]{x}}=\dfrac{x+4}{\sqrt[]{x}}\)
Vì \(x>0;x+4>4\)
\(\Rightarrow P=\dfrac{x+4}{\sqrt[]{x}}>4\)
⇒ Không có giá trị nhỏ nhất


Có : \(x-2y-\sqrt{xy}+\sqrt{x}-2\sqrt{y}=0\)
\(\Leftrightarrow\left(\sqrt{x}-2\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)+\sqrt{x}-2\sqrt{y}=0\)
\(\Leftrightarrow\left(\sqrt{x}-2\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}+1\right)=0\)
\(\Leftrightarrow\sqrt{x}=2\sqrt{y}\) (Do \(\sqrt{x}+\sqrt{y}+1>0,\forall x;y>0\))
\(\Leftrightarrow x=4y\)
Khi đó \(P=\dfrac{7y}{\left(2\sqrt{y}+3\sqrt{y}\right).\left(\sqrt{x}+2\sqrt{y}\right)}\)
\(=\dfrac{7y}{5\sqrt{y}.4\sqrt{y}}=\dfrac{7}{20}\)

1: ĐKXĐ: (x-3)(x+1)>=0
=>x>=3 hoặc x<=-1
2: ĐKXĐ: x(x+2)>=0
=>x>=0 hoặc x<=-2
3: ĐKXĐ: (x-4)(x+4)>=0
=>x>=4 hoặc x<=-4
4: DKXĐ: (x-2)(x+2)>=0
=>x>=2 hoặc x<=-2
6: ĐKXĐ: (x-6)(x+6)>=0
=>x>=6 hoặc x<=-6
7: ĐKXĐ: 2x-16>=0
=>x>=8
8: ĐKXĐ: x(x-1)>=0
=>x>=1 hoặc x<=0

\(x+y=1\Rightarrow x=1-y\)
\(C=x^2+y^2+xy=\left(1-y\right)^2+y^2+\left(1-y\right)y\)
\(=y^2-y+1\)\(=\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall y\)
=>minC=\(\dfrac{3}{4}\) \(\Leftrightarrow y=\dfrac{1}{2}\Rightarrow x=\dfrac{1}{2}\)
Ta có :
\(x+y=1\Rightarrow\left(x+y\right)^2=1\)
\(\Leftrightarrow x^2+2xy+y^2=1\)
\(\Leftrightarrow x^2+xy+y^2=1-xy\ge1-\left(\dfrac{x+y}{2}\right)^2=1-\dfrac{1}{4}=\dfrac{3}{4}\)
Hay \(C \ge \dfrac{3}{4}\)
Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)

\(P=\dfrac{x+2\sqrt{x}+x-2\sqrt{x}}{x-4}.\dfrac{x-4}{-2\sqrt{x}}=\dfrac{2x}{-2\sqrt{x}}=-\sqrt{x}\)
\(P=-\sqrt{x}=-\sqrt{4}=-2\left(đpcm\right)\)

P = \(\left[x+2sprt\left(x\right)+5\right]\backslash\left[sprt\left(x\right)+1\right] \) là sao bn
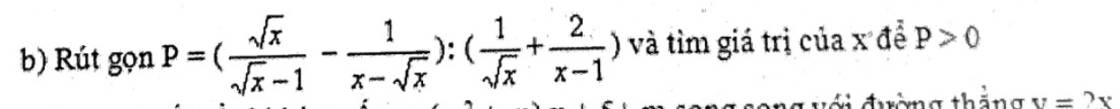 Tìm giúp em giá trị của x ạ. E xin cảm ơn
Tìm giúp em giá trị của x ạ. E xin cảm ơn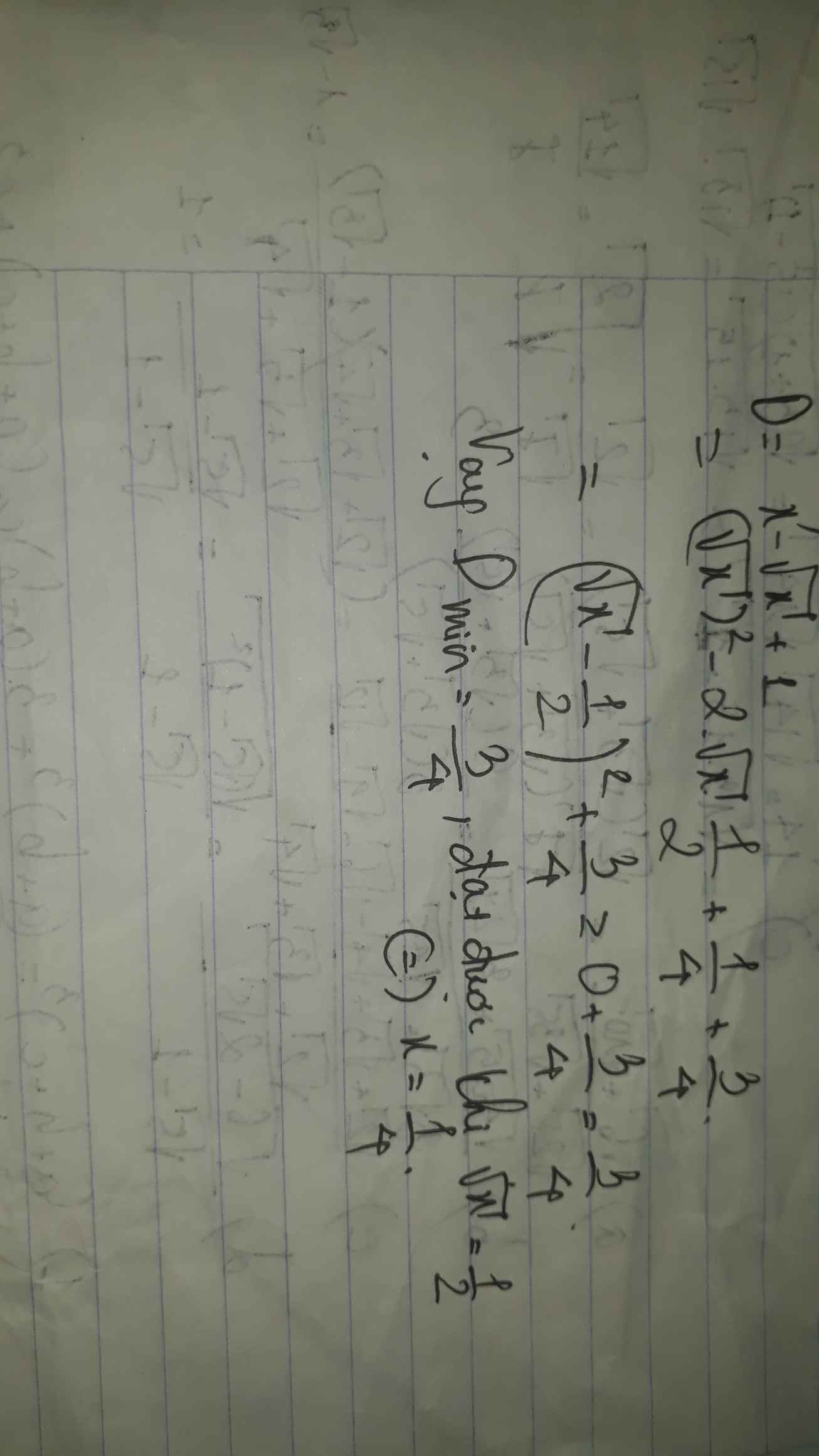
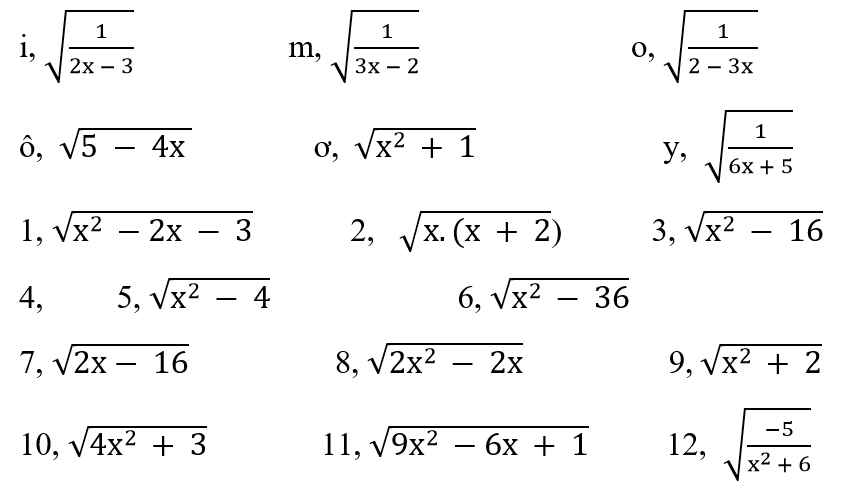

\(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right):\left(\dfrac{1}{\sqrt{x}}+\dfrac{2}{x-1}\right)\)
\(=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\left(\dfrac{1}{\sqrt{x}}+\dfrac{2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{x-1+2\sqrt{x}}{\sqrt{x}\left(x-1\right)}\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{x-1+2\sqrt{x}}\)
\(=\dfrac{x-1}{x-1+2\sqrt{x}}\)
Để \(P>0\)
\(\Rightarrow\dfrac{x-1}{x-1+2\sqrt{x}}>0\)
\(TH_1:x-1>0\Leftrightarrow x>1\)
\(TH_2:x-1+2\sqrt{x}>0\Leftrightarrow\left(\sqrt{x}+1\right)^2< 2\)
\(\Leftrightarrow-\sqrt{2}-1< \sqrt{x}< \sqrt{2}-1\)
\(\Leftrightarrow0< x< 3-2\sqrt{2}\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{x-1+2\sqrt{x}}{\sqrt{x}\left(x-1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}}\cdot\dfrac{\sqrt{x}\left(x-1\right)}{x+2\sqrt{x}-1}\)
\(=\dfrac{\left(x-1\right)\left(\sqrt{x}+1\right)}{x+2\sqrt{x}-1}\)
Để P>0 thì (x-1)/(x+2căn x-1)>0
TH1: x-1>0 và x+2căn x-1>0
=>x>1
TH2: x-1<0 và x+2căn x-1<0
=>0<x<1 và (căn x+1)^2<2
=>0<x<1và \(-\sqrt{2}< \sqrt{x}+1< \sqrt{2}\)
=>\(\left\{{}\begin{matrix}0< x< 1\\-\sqrt{2}-1< \sqrt{x}< \sqrt{2}-1\end{matrix}\right.\Leftrightarrow0< x< 3-2\sqrt{2}\)