Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
Đặt: (d): y = (m+5)x + 2m - 10
Để y là hàm số bậc nhất thì: m + 5 # 0 <=> m # -5
Để y là hàm số đồng biến thì: m + 5 > 0 <=> m > -5
(d) đi qua A(2,3) nên ta có:
3 = (m+5).2 + 2m - 10
<=> 2m + 10 + 2m - 10 = 3
<=> 4m = 3
<=> m = 3/4
(d) cắt trục tung tại điểm có tung độ bằng 9 nên ta có:
9 = (m+5).0 + 2m - 10
<=> 2m - 10 = 9
<=> 2m = 19
<=> m = 19/2
(d) đi qua điểm 10 trên trục hoành nên ta có:
0 = (m+5).10 + 2m - 10
<=> 10m + 50 + 2m - 10 = 0
<=> 12m = -40
<=> m = -10/3
(d) // y = 2x - 1 nên ta có:
\(\hept{\begin{cases}m+5=2\\2m-10\ne-1\end{cases}}\) <=> \(\hept{\begin{cases}m=-3\\m\ne\frac{9}{2}\end{cases}}\) <=> \(m=-3\)

1. a) Để hs trên là hs bậc nhất khi và chỉ khi a>0 --> 3+2k>0 --> k >\(\frac{-3}{2}\)
b) Vì đths cắt trục tung tại điểm có tung độ = 5 --> x=0, y=5
Thay y=5 và x=0 vào hs và tìm k
2. a) Tự vẽ
b) Hệ số góc k=\(\frac{-a}{b}=\frac{-2}{4}=\frac{-1}{2}\)
c) Phương trình hoành độ giao điểm là:\(2x+4=-x-2\)(tìm x rồi thay x vào 1 trong 2 pt --> tính y) (x=-2; y=0)
3. Vì 3 đg thẳng đồng quy -->d1 giao d2 giao d3 tại 1 điểm (giao kí hiệu là chữ U ngược)
Tính tọa độ giao điểm của d1 và d2 --> x=2;y=1
Điểm (2;1) thuộc d3 --> Thay x=2 và y=1 vào d3 -->m=3


1: Khi m=2 thì y=(2-1)x+2=x+2
Vẽ đồ thị:
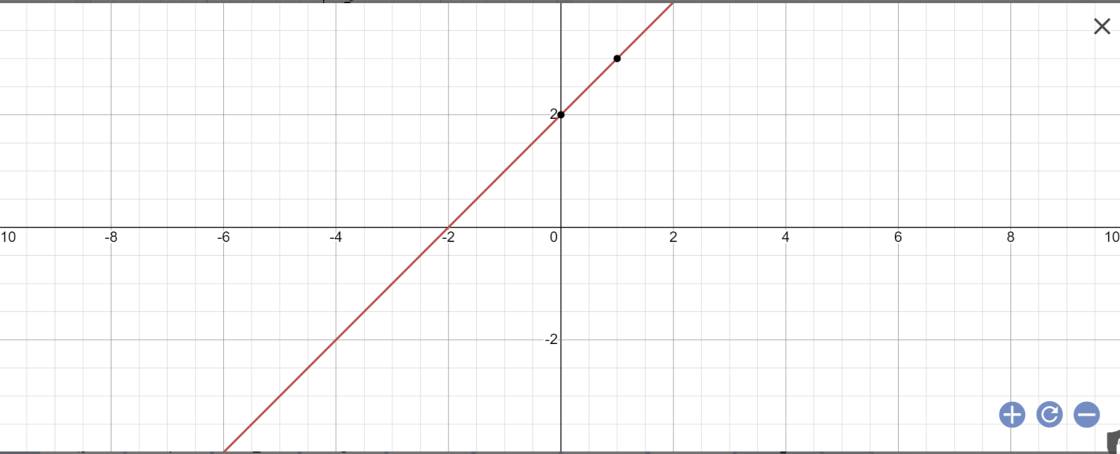
\(tan\alpha=a=1\)
=>\(\alpha=45^0\)
2: Thay x=1 và y=0 vào (d), ta được:
\(1\left(m-1\right)+m=0\)
=>2m-1=0
=>m=1/2
3:
y=(m-1)x+m
=mx-x+m
=m(x+1)-x
Điểm mà (d) luôn đi qua có tọa độ là:
\(\left\{{}\begin{matrix}x+1=0\\y=-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)