DL
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 7 2023
\(P=\sqrt[]{x}+\dfrac{3}{\sqrt[]{x}-1}\left(x>1\right)\)
\(P=\sqrt[]{x}-1+\dfrac{3}{\sqrt[]{x}-1}+1\)
Áp dụng bất đẳng thức Cauchy cho 2 số \(\sqrt[]{x}-1;\dfrac{3}{\sqrt[]{x}-1}\) ta được :
\(\sqrt[]{x}-1+\dfrac{3}{\sqrt[]{x}-1}\ge2\sqrt[]{\sqrt[]{x}-1.\dfrac{3}{\sqrt[]{x}-1}}\)
\(\Rightarrow\sqrt[]{x}-1+\dfrac{3}{\sqrt[]{x}-1}\ge2\sqrt[]{3}\)
\(\Rightarrow P=\sqrt[]{x}-1+\dfrac{3}{\sqrt[]{x}-1}+1\ge2\sqrt[]{3}+1\)
\(\Rightarrow Min\left(P\right)=2\sqrt[]{3}+1\)
17 tháng 7 2023
\(P=\dfrac{x+5}{\sqrt[]{x}+2}=\dfrac{x-4+9}{\sqrt[]{x}+2}=\dfrac{\left(\sqrt[]{x}+2\right)\left(\sqrt[]{x}-2\right)+9}{\sqrt[]{x}+2}\)
\(=\left(\sqrt[]{x}-2\right)+\dfrac{9}{\sqrt[]{x}+2}=\left(\sqrt[]{x}+2\right)+\dfrac{9}{\sqrt[]{x}+2}-4\)
Áp dụng bất đẳng thức Cauchy cho 2 số \(\left(\sqrt[]{x}+2\right);\dfrac{9}{\sqrt[]{x}+2}\left(x\ge0\right)\)
\(\left(\sqrt[]{x}+2\right)+\dfrac{9}{\sqrt[]{x}+2}\ge2\sqrt[]{\left(\sqrt[]{x}+2\right).\dfrac{9}{\sqrt[]{x}+2}}=2.3=6\)
\(\Rightarrow P=\left(\sqrt[]{x}+2\right)+\dfrac{9}{\sqrt[]{x}+2}-4\ge6-4=2\)
\(\Rightarrow P\ge2\Rightarrow Min\left(P\right)=2\)
17 tháng 7 2023
Bạn xem lại đề có phải \(P=x+\dfrac{5}{\sqrt[]{x}+2}\) không?
5 tháng 2 2022
1: ĐKXĐ: (x-3)(x+1)>=0
=>x>=3 hoặc x<=-1
2: ĐKXĐ: x(x+2)>=0
=>x>=0 hoặc x<=-2
3: ĐKXĐ: (x-4)(x+4)>=0
=>x>=4 hoặc x<=-4
4: DKXĐ: (x-2)(x+2)>=0
=>x>=2 hoặc x<=-2
6: ĐKXĐ: (x-6)(x+6)>=0
=>x>=6 hoặc x<=-6
7: ĐKXĐ: 2x-16>=0
=>x>=8
8: ĐKXĐ: x(x-1)>=0
=>x>=1 hoặc x<=0
KH
2
ML
15 tháng 5 2023
\(T=\dfrac{\sqrt{27}+3}{\sqrt{3}}=\dfrac{3\sqrt{3}+3}{\sqrt{3}}=\dfrac{3\left(\sqrt{3}+1\right)}{\sqrt{3}}=\sqrt{3}\left(\sqrt{3}+1\right)=3+\sqrt{3}\)
15 tháng 5 2023
Dạ √27 + 3 / √3 ạ 3 với căn 3 là chung với nhau ý ạ chứ ko phải như trên ý ạ
19 tháng 2 2021
a) Ta có: \(M=\left(\dfrac{\sqrt{x}-3}{\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\right)\cdot\dfrac{x+3\sqrt{x}}{7-\sqrt{x}}\)
\(=\left(\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}-\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\right)\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{7-\sqrt{x}}\)
\(=\dfrac{x-9-\left(x-2\sqrt{x}+\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{7-\sqrt{x}}\)
\(=\dfrac{x-9-x+\sqrt{x}+2}{\left(\sqrt{x}-2\right)}\cdot\dfrac{1}{-\left(\sqrt{x}-7\right)}\)
\(=\dfrac{\sqrt{x}-7}{\sqrt{x}-2}\cdot\dfrac{-1}{\sqrt{x}-7}\)
\(=\dfrac{-1}{\sqrt{x}-2}\)(1)
b) Ta có: \(x^2-4x=0\)
\(\Leftrightarrow x\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=4\left(loại\right)\end{matrix}\right.\)
Thay x=0 vào biểu thức (1), ta được:
\(M=\dfrac{-1}{\sqrt{0}-2}=\dfrac{-1}{-2}=\dfrac{1}{2}\)
Vậy: Khi \(x^2-4x=0\) thì \(M=\dfrac{1}{2}\)
11 tháng 3 2020
ĐK: \(x\ge0\)
+) Với x = 0 => A = 0
+) Với x khác 0
Ta có: \(\frac{1}{A}=\frac{3}{4}\sqrt{x}-\frac{3}{4}+\frac{3}{4\sqrt{x}}=\frac{3}{4}\left(\sqrt{x}+\frac{1}{\sqrt{x}}\right)-\frac{3}{4}\ge\frac{3}{4}.2-\frac{3}{4}=\frac{3}{4}\)
=> \(A\le\frac{4}{3}\)
Dấu "=" xảy ra <=> \(\sqrt{x}=\frac{1}{\sqrt{x}}\)<=> x = 1
Vậy max A = 4/3 tại x = 1
Còn có 1 cách em quy đồng hai vế giải đenta theo A thì sẽ tìm đc cả GTNN và GTLN
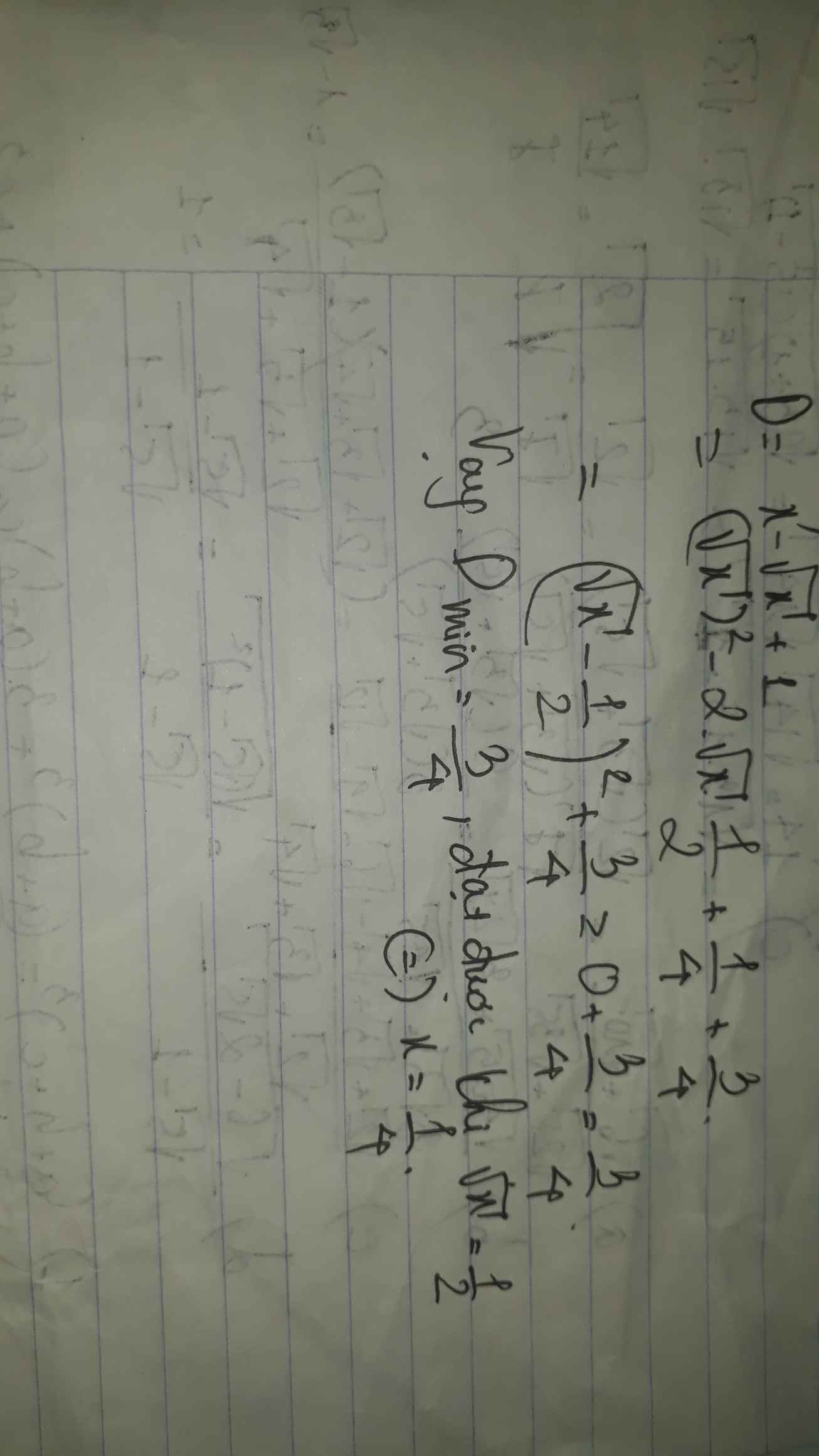
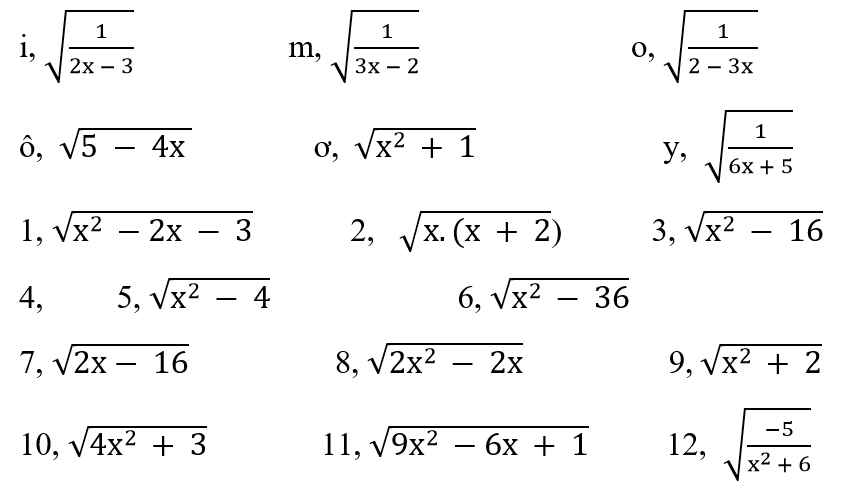
ĐKXĐ : \(x>0\)
Áp dụng bất đẳng thức Cauchy cho 2 số dương \(\sqrt{x};\dfrac{4}{\sqrt{x}}\) ta có
\(P=\sqrt{x}+\dfrac{4}{\sqrt{x}}\ge2\sqrt{\sqrt{x}.\dfrac{4}{\sqrt{x}}}=4\)
Dấu "=" xảy ra khi \(\sqrt{x}=\dfrac{4}{\sqrt{x}}\Leftrightarrow x=4\)
\(P=\sqrt[]{x}+\dfrac{4}{\sqrt[]{x}}\left(x>0\right)\)
\(P=\dfrac{x+4}{\sqrt[]{x}}=\dfrac{x+4}{\sqrt[]{x}}\)
Vì \(x>0;x+4>4\)
\(\Rightarrow P=\dfrac{x+4}{\sqrt[]{x}}>4\)
⇒ Không có giá trị nhỏ nhất