Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có A = 5x2 - 2xy + 2y2 - 4x + 2y + 3
=> 2A = 10x2 - 4xy + 4y2 - 8x + 4y + 6
= (x2 - 4xy + 4y2) - 2(x - 2y) + 1 + 9x2 - 6x + 1 + 4
= \(\left(x-2y\right)^2-2\left(x-2y\right)+1+9\left(x^2-\frac{2}{3}x+\frac{1}{9}\right)+4\)
\(=\left(x-2y-1\right)^2+9\left(x-\frac{1}{3}\right)^2+4\)\(\ge4\)
=> A \(\ge\)2
Dấu "=" xảy ra <=> \(\hept{\begin{cases}x-2y-=0\\x-\frac{1}{3}=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x-2y=1\\x=\frac{1}{3}\end{cases}}\Leftrightarrow\hept{\begin{cases}y=-\frac{1}{3}\\x=\frac{1}{3}\end{cases}}\)
Vậy khi x = 1/3 ; y = -1/3 thì A đạt GTNN
\(A=5x^2+2y^2-2xy-4x+2y\)\(+3\)
\(=\left(x^2-2xy+y^2\right)+\)\(\left(4x^2-4x+1\right)+\)\(\left(y^2+2y+1\right)+1\)
\(Tacó\)

\(A=2x^2+2xy+y^2-2x+2y+1\)
\(=x^2+x^2+2xy+y^2+2x-4x+2y+1+4-4\)
\(=\left(x^2+y^2+1+2xy+2x+2y\right)+\left(x^2-4x+4\right)-4\)
\(=\left(x+y+1\right)^2+\left(x-2\right)^2-4\)
\(\left\{{}\begin{matrix}\left(x+y+1\right)^2\ge0\\\left(x-2\right)^2\ge0\end{matrix}\right.\)
\(\Rightarrow\) Giá trị nhỏ nhất của A là: -4

\(2x^2+2xy+5y^2=\left(x+2y\right)^2+\left(x-y\right)^2\ge\left(x+2y\right)^2\)
\(\Rightarrow P\ge\dfrac{x+2y}{3x+y+5z}+\dfrac{y+2z}{3y+z+5x}+\dfrac{z+2x}{3x+x+5y}\)
\(\Rightarrow P\ge\dfrac{\left(x+2y\right)^2}{\left(x+2y\right)\left(3x+y+5z\right)}+\dfrac{\left(y+2z\right)^2}{\left(y+2z\right)\left(3y+z+5x\right)}+\dfrac{\left(z+2x\right)^2}{\left(z+2x\right)\left(3x+x+5y\right)}\)
\(\Rightarrow P\ge\dfrac{\left(x+2y\right)^2}{3x^2+2y^2+7xy+5xz+10yz}+\dfrac{\left(y+2z\right)^2}{3y^2+2z^2+7yz+5xy+10xz}+\dfrac{\left(z+2x\right)^2}{3z^2+2x^2+7xz+5yz+10xy}\)
\(\Rightarrow P\ge\dfrac{\left(x+2y+y+2z+z+2x\right)^2}{5\left(x^2+y^2+z^2\right)+22\left(xy+xz+yz\right)}\)
\(\Rightarrow P\ge\dfrac{9\left(x+y+z\right)^2}{5\left(x+y+z\right)^2+12\left(xy+xz+yz\right)}\ge\dfrac{9\left(x+y+z\right)^2}{5\left(x+y+z\right)^2+\dfrac{12\left(x+y+z\right)^2}{3}}\)
\(\Rightarrow P\ge1\)
\(\Rightarrow P_{min}=1\) khi \(x=y=z\)

\(\sqrt{2x^2+2y^2}\ge\sqrt{\left(x+y\right)^2}=10\)
Đạt được khi x = y = 5

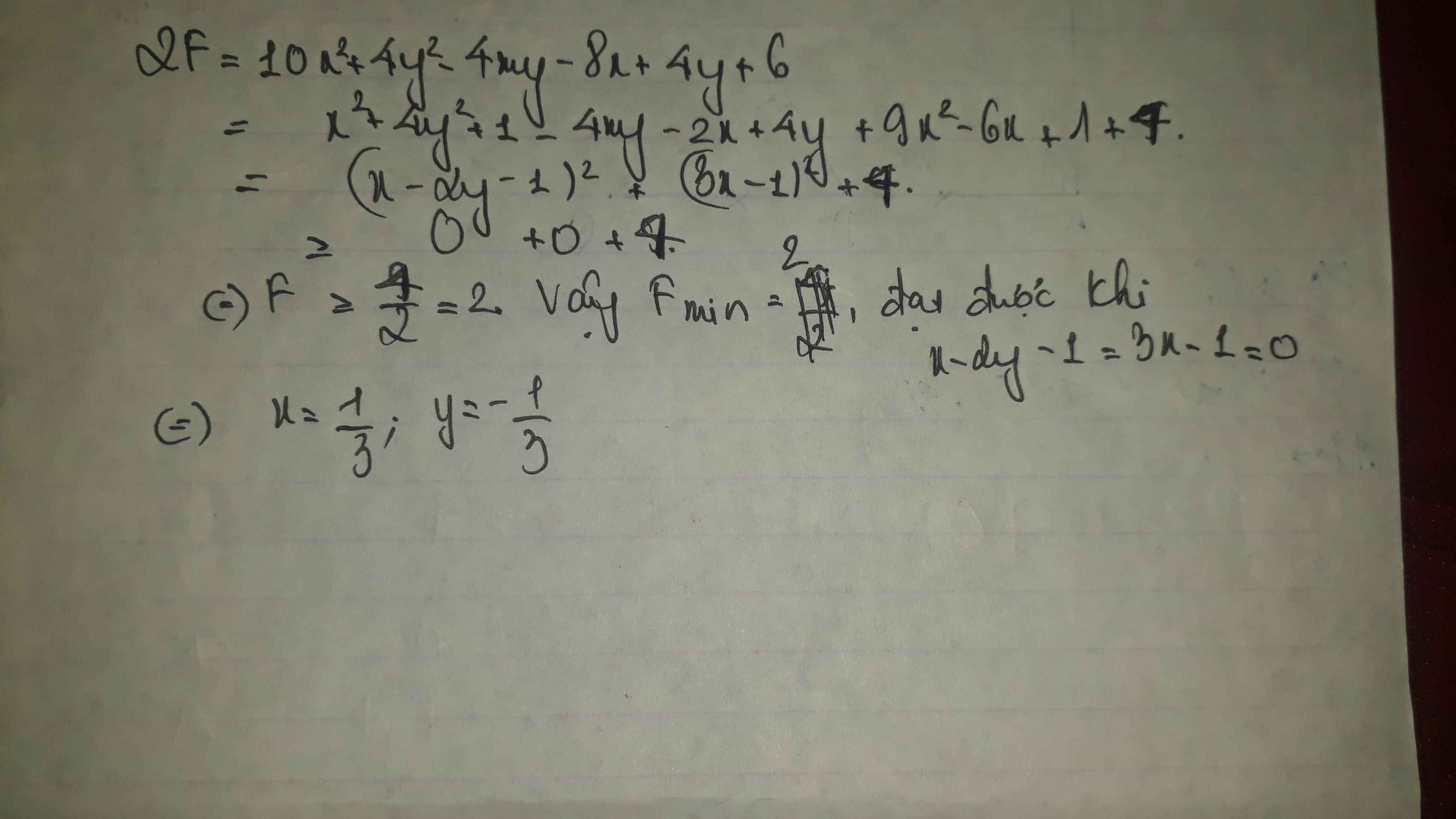
\(M=5x^2+y^2-2x+2y+2xy+2004\)
\(=\left(x^2+2x+1\right)+2y\left(x+1\right)+y^2+4x^2-4x+1+2002\)
\(=\left(x+1\right)^2+2y\left(x+1\right)+y^2+\left(2x-1\right)^2+2002\)
\(=\left(x+1+y\right)^2+\left(2x-1\right)^2+2003\ge2002\) với mọi x,y
=> \(M_{min}=2002\Leftrightarrow\left\{{}\begin{matrix}x+y+1=0\\2x-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{3}{2}\\x=\dfrac{1}{2}\end{matrix}\right.\)
Vậy \(M_{min}=2002\)
Dòng 4 toi viết nhầm nha, là +2002