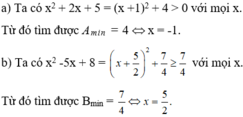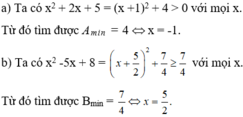
a) A =
x...">
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời. a, ĐKXĐ: \(\hept{\begin{cases}5x+25\ne0\\x\ne0\\x^2+5x\ne0\end{cases}\Rightarrow\hept{\begin{cases}5\left(x+5\right)\ne0\\x\ne0\\x\left(x+5\right)\ne0\end{cases}\Rightarrow}}\hept{\begin{cases}x\ne0\\x\ne-5\end{cases}}\) b, \(P=\frac{x^2}{5x+25}+\frac{2x-10}{x}+\frac{50+5x}{x^2+5x}\) \(=\frac{x^3}{5x\left(x+5\right)}+\frac{5\left(2x-10\right)\left(x+5\right)}{5x\left(x+5\right)}+\frac{\left(50+5x\right).5}{5x\left(x+5\right)}\) \(=\frac{x^3+10\left(x-5\right)\left(x+5\right)+250+25x}{5x\left(x+5\right)}\) \(=\frac{x^3+10x^2+25x}{5x\left(x+5\right)}=\frac{x\left(x+5\right)^2}{5x\left(x+5\right)}=\frac{x+5}{5}\) c, \(P=-4\Rightarrow\frac{x+5}{5}=-4\Rightarrow x+5=-20\Rightarrow x=-25\) d, \(\frac{1}{P}\in Z\Rightarrow\frac{5}{x+5}\in Z\Rightarrow5⋮\left(x+5\right)\Rightarrow x+5\inƯ\left(5\right)=\left\{-5;-1;1;5\right\}\Rightarrow x\in\left\{-10;-6;-4;0\right\}\) Mà x khác 0 (ĐKXĐ của P) nên \(x\in\left\{-10;-6;-4\right\}\) a) \(ĐKXĐ:\hept{\begin{cases}5x+25\ne0\\x\ne0\\x^2+5x\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ne0\\x\ne-5\end{cases}}\) b) \(P=\frac{x^2}{5x+25}+\frac{2x-10}{x}+\frac{50+5x}{x^2+5x}\) \(P=\frac{x^3}{5x\left(x+5\right)}+\frac{10x^2-250}{5x\left(x+5\right)}+\frac{250+25x}{5x\left(x+5\right)}\) \(P=\frac{x^3+10x^2+25x}{5x\left(x+5\right)}=\frac{x\left(x+5\right)^2}{5x\left(x+5\right)}=\frac{x+5}{5}\) c) \(P=4\Leftrightarrow\frac{x+5}{5}=4\Leftrightarrow x+5=20\Leftrightarrow x=15\) d) \(\frac{1}{P}=\frac{5}{x+5}\in Z\Leftrightarrow5⋮x+5\) \(\Leftrightarrow x+5\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\) Lập bảng nhé e) \(Q=P+\frac{x+25}{x+5}=\frac{x+30}{x+5}=1+\frac{25}{x+5}\) \(Q_{min}\Leftrightarrow\frac{25}{x+5}_{min}\) b)\(C=\frac{5x-19}{x-4}=\frac{5x-20+1}{x-4}=\frac{5\left(x-4\right)+1}{x-4}=5+\frac{1}{x-4}\) Để C đạt giá trị nhỏ nhất => 1/x-5 phải đạt giá trị nhỏ nhất => 1/x-5=-1 =>x-5=-1 =>x=4 Giá trị nhỏ nhất của C là : 5 - 1 = 4 <=> x = 4 a, \(A=x^2+x+1=\left(x^2+x+\frac{1}{4}\right)+\frac{3}{4}=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\) Vì \(\left(x+\frac{1}{2}\right)^2\ge0\Rightarrow A=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\) Dấu "=" xảy ra khi x=-1/2 Vậy Amin=3/4 khi x=-1/2 b,\(B=2x^2-5x-2\) \(\Rightarrow2B=4x^2-10x-4=\left(4x^2-10x+\frac{25}{4}\right)-\frac{41}{4}=\left(2x-\frac{5}{2}\right)^2-\frac{41}{4}\) Vì \(\left(2x-\frac{5}{2}\right)^2\ge0\Rightarrow2B=\left(2x-\frac{5}{2}\right)^2-\frac{41}{4}\ge-\frac{41}{4}\Rightarrow B\ge-\frac{41}{8}\) Dấu "=" xảy ra khi x=5/4 Vậy Bmin=-41/8 khi x=5/4 c,\(C=x^2+5y^2+2xy-y+3=\left(x^2+2xy+y^2\right)+\left(4y^2-y+\frac{1}{16}\right)+\frac{47}{16}=\left(x+y\right)^2+\left(2y-\frac{1}{4}\right)^2+\frac{47}{16}\) Vì\(\hept{\begin{cases}\left(x+y\right)^2\ge0\\\left(2y-\frac{1}{4}\right)^2\ge0\end{cases}}\Rightarrow\left(x+y\right)^2+\left(2y-\frac{1}{4}\right)^2\ge0\) \(\Rightarrow C=\left(x+y\right)^2+\left(2y-\frac{1}{4}\right)^2+\frac{47}{16}\ge\frac{47}{16}\) Dấu "=" xảy ra khi \(\hept{\begin{cases}x+y=0\\2y-\frac{1}{4}=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=\frac{-1}{8}\\y=\frac{1}{8}\end{cases}}}\) Vậy Cmin=47/16 khi x=-1/8,y=1/8 a) \(A=x^2-6x+11\) \(\Rightarrow A=x^2-6x+9+2\) \(\Rightarrow A=\left(x-3\right)^2+2\) Ta có: \(\left(x-3\right)^2\ge0\forall x\) \(\Rightarrow\left(x-3\right)^2+2\ge2\forall x\) Dấu "=" xảy ra \(\Leftrightarrow\) x = 3 Vậy \(MIN\) \(A=2\Leftrightarrow x=3\) b) \(B=2x^2+10x-1\) \(\Rightarrow B=2\left(x^2+5\right)-1\) \(\Rightarrow B=2\left(x^2+2\cdot\dfrac{5}{2}\cdot x+\dfrac{25}{4}\right)-\dfrac{25}{2}-1\) \(\Rightarrow B=2\left(x^2+2\cdot\dfrac{5}{2}\cdot x+\dfrac{25}{4}\right)-\dfrac{23}{2}\) Ta có: \(2\left(x^2+2\cdot\dfrac{5}{2}\cdot x+\dfrac{25}{4}\right)\ge0\forall x\) \(\Rightarrow2\left(x^2+2\cdot\dfrac{5}{2}\cdot x+\dfrac{25}{4}\right)-\dfrac{23}{2}\ge-\dfrac{23}{2}\forall x\) Dấu "=" xảy ra \(\Leftrightarrow\) x = \(\dfrac{-5}{2}\) Vậy \(MIN\) \(B=\dfrac{-23}{2}\Leftrightarrow x=\dfrac{-5}{2}\) c) \(C=5x-x^2\) \(\Rightarrow C=-\left(x^2-5x\right)\) \(\Rightarrow C=-\left(x^2-2\cdot\dfrac{5}{2}\cdot x+\dfrac{25}{4}\right)+\dfrac{25}{4}\) \(\Rightarrow C=-\left(x-\dfrac{5}{2}\right)^2+\dfrac{25}{4}\) Ta có: \(-\left(x-\dfrac{5}{2}\right)^2\le0\forall x\) \(\Rightarrow-\left(x-\dfrac{5}{2}\right)^2+\dfrac{25}{4}\le\dfrac{25}{4}\forall x\) Dấu "=" xảy ra \(\Leftrightarrow\) x = \(\dfrac{5}{2}\) Vậy \(MAX\) \(C=\dfrac{25}{4}\Leftrightarrow x=\dfrac{5}{2}\) \(B=\frac{x^2-2}{x^2+1}=\frac{x^2+1-3}{x^2+1}=1-\frac{3}{x^2+1}\) \(B_{min}\Rightarrow\left(\frac{3}{x^2+1}\right)_{max}\Rightarrow\left(x^2+1\right)_{min}\) \(x^2+1\ge1\). dấu = xảy ra khi x2=0 => x=0 Vậy \(B_{min}\Leftrightarrow x=0\) ta có: \(x^2+2x-2=x^2+2x+1^2-3=\left(x+1\right)^2-3\ge-3\) dấu = xảy ra khi \(x+1=0\) \(\Rightarrow x=-1\) Vậy\(\left(x^2+2x-2\right)_{min}\Leftrightarrow x=-1\) \(1,a,A=x^2-6x+25\) \(=x^2-2.x.3+9-9+25\) \(=\left(x-3\right)^2+16\) Ta có : \(\left(x-3\right)^2\ge0\)Với mọi x \(\Rightarrow\left(x-3\right)^2+16\ge16\) Hay \(A\ge16\) \(\Rightarrow A_{min}=16\) \(\Leftrightarrow x=3\) A=x^2+5x+7 A=x^2+2.x.5/2+25/4+3/4 A=(x+5/2)^2+3/4>= 3/4 Vậy Min A=3/4 <=> x=-5/2 ấ ở đây nhé ! Mình có làm bài tìm giá trị lớn nhất trong đây rùi nhé !