TM
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
14 tháng 2 2018
Chọn C.
Theo giả thiết ta có:
P = ( sina + sinb) 2 + ( cosa + cosb) 2
= sin2a + 2.sina.sinb + sin2b + cos2a + 2cosa. cosb + cos2b
= 2 + 2( sina.sinb + cos a. cosb)
= 2 + 2.cos( a - b) ( sử dụng công thức cộng)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 6 2020
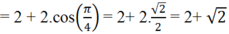
\(A=cos^2a+cos^2b+2cosa.cosb+sin^2a+sin^2b+2sina.sinb\)
\(=cos^2a+sin^2a+cos^2b+sin^2b+2\left(cosa.cosb+sina.sinb\right)\)
\(=2+2cos\left(a-b\right)=2+2cos\frac{\pi}{3}=3\)
\(\left(cosa+sina\right)^2=\frac{36}{25}\Leftrightarrow1+2sina.cosa=\frac{36}{25}\)
\(\Rightarrow sin2a=\frac{36}{25}-1=\frac{11}{25}\)
\(cos2a=cos^2a-sin^2a=\left(cosa-sina\right)\left(cosa+sina\right)>0\)
\(\Rightarrow cos2a=\sqrt{1-sin^22a}=\frac{6\sqrt{14}}{25}\)
8 tháng 5 2018
[1-2sina/2cosa/2+(2cos^2a/2 - 1)]/[1-2sina/2cosa/2-1+2sin^a]
=2cosa/2(cosa/2-sina/2)/[2sina/2(sina/2-cosa/2)]
= -cota/2
LH
9 tháng 10 2016
\(sina+cosa=\sqrt{2}\Leftrightarrow\left(sina+cosa\right)^2=2\\ \)
\(\Leftrightarrow\sin^2a+2\sin a.cosa+cos^2a=2\)
\(\Leftrightarrow1+2.sina.cosa=2\)
\(\Leftrightarrow2.sina.cosa=2-1=1\)
\(\Leftrightarrow\sin a.cosa=\frac{1}{2}\)
Vậy P=sina.cosa=\(\frac{1}{2}\)
\(Q=\sin^4a+cos^4a\)
\(\Leftrightarrow\left(sin^2a\right)^2+\left(cos^2a\right)^2\)
\(\Leftrightarrow\left(sin^2a+cos^2a\right)^2-2.sin^2a.cos^2a\)
\(\Leftrightarrow1^2-2.sin^2a.cos^2a\) tách tiếp rồi thế vào là được .tương tự phàn P ý
còn R thì tách sin^3a=sin^2a+sina tương tự cos mũ 3 a cụng vậy
theo tớ là như thế còn có sai thì đừng có ném đá ném gạch na
CM
20 tháng 7 2019
Chọn B.
Ta có: 
Nên (sina + cosa)2 =2 hay sin2a + cos2a + 2 sina.cosa = 2
Suy ra sina.cosa = ½.
Khi đó: sin4a + cos4a = (sin2a + cos2a)2 - 2sin2a.cos2a = 1 - 2.(1/2)2 = ½.
HP
27 tháng 1 2021
Áp dụng BĐT BSC và BĐT \(2\left(x^2+y^2\right)\ge\left(x+y\right)^2\):
\(A=x\sqrt{y+1}+y\sqrt{x+1}\)
\(\Rightarrow A^2=\left(x\sqrt{y+1}+y\sqrt{x+1}\right)^2\)
\(\le\left(x^2+y^2\right)\left(x+y+2\right)\)
\(\le\left(x^2+y^2\right)\left[\sqrt{2\left(x^2+y^2\right)}+2\right]=\sqrt{2}+2\)
\(\Rightarrow-\sqrt{\sqrt{2}+2}\le A\le\sqrt{\sqrt{2}+2}\)
\(\Rightarrow minA=\sqrt{\sqrt{2}+2}\Leftrightarrow x=y=-\dfrac{1}{\sqrt{2}}\)
\(A=sina+\sqrt{3}cosa=2\left(\frac{1}{2}sina+\frac{\sqrt{3}}{2}cosa\right)\)
\(2=\left(sina.cos\frac{\pi}{3}+cosa.sin\frac{\pi}{3}\right)=2sin\left(a+\frac{\pi}{3}\right)\ge-2\)
\(\Rightarrow A_{min}=-2\) khi \(sin\left(a+\frac{\pi}{3}\right)=-1\Rightarrow a=-\frac{5\pi}{6}+k2\pi\)