Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
y ' = 4 x 3 - 4 m 2 + 1 x y ' = 0 ⇔ x = 0 x = ± m 2 + 1
Dễ thấy hàm số đã cho có 3 điểm cực trị với mọi m.
Với x C T = ± m 2 + 1 ⇒ giá trị cực tiểu y C T = - m 2 + 1 + 1
Ta có m 2 + 1 2 ≥ 1 ⇒ y C T ≤ 0 m a x y C T = 0 ⇔ m 2 + 1 = 1 ⇔ m = 0
Đáp án A
giả sử : \(\frac{mx+m}{\left(m+1\right)x-m+2}>0\)\(,\text{∀}x\in\left[0;2\right]\)
\(\Rightarrow\frac{m.0+m}{\left(m+1\right).0-m+2}>0\) \(\Rightarrow\frac{m}{2-m}>0\)
\(\Rightarrow0\)\(<\)\(m<\)\(2\)
ngược lại \(0<\)\(m<2\) thì:
\(mx+m>0,\text{∀}x\in\left[0;2\right]\)
\(\left(m+1\right)x\ge0>m-2,\)\(\text{∀}x\in\left[0;2\right]\)
\(\Rightarrow\left(m+1\right)x-m+2>0,\text{∀}x\in\left[0;2\right]\)
\(\Rightarrow\frac{mx+m}{\left(m+1\right)x-m+2}>0,\text{∀}x\in\left[0;2\right]\)
vậy: \(0\)\(<\)\(m<\)\(2\) là kết quả cần tìm
*x2+bx+c=0
\(\Delta=b^2-4c=b^2-4.\left(2b-4\right)=b^2-8b+16=\left(b-4\right)^2\)=>\(\sqrt{\Delta}=\left|b-4\right|\)
Với (b-4)2=0 =>b=4 =>c=4
PT có 1 nghiệm kép: \(x_1=x_2=-2\)
Với\(\Delta=\) (b-4)2>0,PT có 2 nghiệm pb: \(x_1=\frac{-b+\left|b-4\right|}{2};x_2=\frac{-b-\left|b-4\right|}{2}\)
Với b>4 thì: \(x_1=-2;x_2=\frac{-2b+4}{2}=-b+2\)
Với b<0 thì: x1=-b+2 ; x2=-2
Vậy khi c=2b-4 và b tùy ý thì PT: x2+bx+c=0 luôn có 1 nghiệm nguyên là -2
Đáp án A
Phương pháp giải:
Tìm tọa độ điểm cực trị của đồ thị hàm số trùng phương và tính diện tích tam giác
Lời giải: TXĐ : D = R
Ta có 
R
Phương trình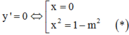 
Hàm số có 3 điểm cực trị ó (*) có 2 nghiệm phân biệt khác 
Khi đó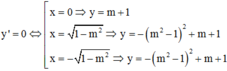 
Gọi 
; 
là ba điểm cực trị. Tam giác ABC cân tại A.
Trung điểm H của BC là 
Và 
Diện tích tam giác ABC là 
Mà 
R suy ra 
Vậy Smax = 1 Dấu bằng xảy ra khi và chỉ khi m = 0
cho 2014=2013+1 thay vào ta có:\(B=x^{2013}-\left(2013+1\right)x^{2012}+\left(2013+1\right)x^{2011}-...-\left(2013+1\right)x^2+\left(2013+1\right)x-1\)
\(=x^{2013}-\left(x+1\right)x^{2012}+\left(x+1\right)x^{2011}-...-\left(x+1\right)x^2+\left(x+1\right)x-1\)
\(=x^{2013}-x^{2013}-x^{2012}+x^{2012}+x^{2011}-...-x^3-x^2+x^2+x-1\)
\(=x-1=2013-1=2012\)
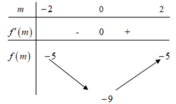
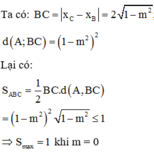
Đáp án B
Ta có y ' = 4 x 3 - 4 m 2 + 1 x , ∀ x ∈ ℝ . Phương trình y ' = 0 ⇔ [ x = 0 x = m 2 + 1 .
Hệ số a > 0 suy ra giá trị cực tiểu của hàm số là y C T = 2 - m 2 + 1 4 ≤ 1
Dấu “=” xảy ra khi và chỉ khi m 2 = 0 ⇒ m = 0 .