Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(0\le\sin^2x\le1\Rightarrow0,5^0\ge0,5^{\sin^2x}\ge0,5^1\)
\(\Leftrightarrow1\ge f\left(x\right)\ge\frac{1}{2}\)
\(\Leftrightarrow\) Max f(x) = 1 khi \(x=k\pi\)
Min f(x) =\(\frac{1}{2}\) khi \(x=\frac{\pi}{2}+k\pi\) \(k\in Z\)
Đặt \(t=\sin^2x\) với \(t\in\left[0;1\right]\Rightarrow f\left(x\right)=0,5^t=g\left(t\right)\) với \(t\in\left[0;1\right]\)
Ta có : \(g'\left(t\right)=0,5^1\ln0,5=-0,5^t\ln2< 0\) với mọi \(t\in\left[0;1\right]\) hàm số nghịch biến với mọi \(t\in\left[0;1\right]\)
\(\Rightarrow0\le t\le1\Rightarrow g\left(0\right)\ge g\left(t\right)\ge g\left(1\right)\Leftrightarrow1\ge g\left(t\right)\ge\frac{1}{2}\)
Vậy Max f(x) = 1 khi \(x=k\pi\)
Min \(f\left(x\right)=\frac{1}{2}\) khi \(x=\frac{\pi}{2}+k\pi\) (k thuộc Z)

\(f\left(x\right)=\dfrac{2x-1}{x-3}=\dfrac{2\left(x-3\right)+5}{x-3}=1+\dfrac{5}{\left(x-3\right)}\)
f(x) có dạng \(y=\dfrac{5}{x}\Rightarrow\) f(x) luôn nghịch biến
Tất nhiên bạn có thể tính đạo hàm --> f(x) <0 mọi x khác -3
f(x) luôn nghich biến [0;2] < -3 thuộc nhánh Bên Phải tiệm cận đứng
\(\Rightarrow\left\{{}\begin{matrix}Max=f\left(0\right)=\dfrac{1}{3}\\Min=f\left(2\right)=-3\end{matrix}\right.\)

Ta có : \(f'\left(x\right)=2x+\frac{2}{1-2x}=\frac{-4x^2+2x+2}{1-2x}=0\Leftrightarrow-4x^2+2x+2=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=-\frac{1}{2}\in\left[-2;0\right]\\x=1\notin\left[-2;0\right]\end{array}\right.\)
Mà :
\(\begin{cases}f\left(-2\right)=4-\ln5;x=-2\\f\left(-\frac{1}{2}\right)=\frac{1}{4}-\ln2=\frac{1-4\ln2}{4};x=-\frac{1}{2}\\\end{cases}\)


a) f(x) = 2x3 – 3x2 – 12x + 1 ⇒ f’(x) = 6x2 – 6x – 12
f’(x) = 0 ⇔ x ∈ {-1, 2}
So sánh các giá trị:
f(x) = -3; f(-1) = 8;
f(2) = -19, f(52)=−332f(52)=−332
Suy ra:
maxx∈[−2,52]f(x)=f(−1)=8minx∈[−2,52]f(x)=f(2)=−19maxx∈[−2,52]f(x)=f(−1)=8minx∈[−2,52]f(x)=f(2)=−19
b) f(x) = x2 lnx ⇒ f’(x)= 2xlnx + x > 0, ∀ x ∈ [1, e] nên f(x) đồng biến.
Do đó:
maxx∈[1,e]f(x)=f(e)=e2minx∈[1,e]f(x)=f(1)=0maxx∈[1,e]f(x)=f(e)=e2minx∈[1,e]f(x)=f(1)=0
c) f(x) = f(x) = xe-x ⇒ f’(x)= e-x – xe-x = (1 – x)e-x nên:
f’(x) = 0 ⇔ x = 1, f’(x) > 0, ∀x ∈ (0, 1) và f’(x) < 0, ∀x ∈ (1, +∞)
nên:
maxx∈[0,+∞)f(x)=f(1)=1emaxx∈[0,+∞)f(x)=f(1)=1e
Ngoài ra f(x) = xe-x > 0, ∀ x ∈ (0, +∞) và f(0) = 0 suy ra
maxx∈[0,+∞)f(x)=f(0)=0maxx∈[0,+∞)f(x)=f(0)=0
d) f(x) = 2sinx + sin2x ⇒ f’(x)= 2cosx + 2cos2x
f’(x) = 0 ⇔ cos 2x = -cosx ⇔ 2x = ± (π – x) + k2π
⇔ x∈{−π+k2π;π3+k2π3}x∈{−π+k2π;π3+k2π3}
Trong khoảng [0,3π2][0,3π2] , phương trình f’(x) = 0 chỉ có hai nghiệm là x1=π3;x2=πx1=π3;x2=π
So sánh bốn giá trị : f(0) = 0; f(π3)=3√32;f(π)=0;f(3π2)=−2f(π3)=332;f(π)=0;f(3π2)=−2
Suy ra:
maxx∈[0,3π2]f(x)=f(π3)=3√32minx∈[0,3π2]f(x)=f(3π2)=−2

Đặt \(t=\log x\) với \(x\in\left[10;1000\right]\Rightarrow t\in\left[1;3\right]\Rightarrow f\left(x\right)=t^2-4t+3=g\left(t\right)\) với \(t\in\left[1;3\right]\)
Ta có : \(g'\left(t\right)=2t-4=0\Leftrightarrow t=2\in\left[1;3\right]\)
Mà : \(\begin{cases}g\left(1\right)=0\\g\left(2\right)=-1\\g\left(3\right)=0\end{cases}\) \(\Rightarrow\begin{cases}Max_{x\in\left[10;1000\right]}f\left(x\right)=0;x=10;x=1000\\Min_{x\in\left[10;1000\right]}f\left(x\right)=0;x=1000\end{cases}\)

1. \(f\left(x\right)=e^x\left(x^2-x-1\right)\) trên đoạn \(\left[0;3\right]\)
Ta có :
\(f'\left(x\right)=e^x\left(x^2-x-1\right)+e^x\left(2x-1\right)=e^x\left(x^2+x-2\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=-2\notin\left[0;3\right]\\x=1\in\left[0;3\right]\end{array}\right.\)
Mà : \(\begin{cases}f\left(0\right)=-1\\f\left(1\right)=-e\\f\left(3\right)=6e^3\end{cases}\) \(\Leftrightarrow\begin{cases}Max_{x\in\left[0;3\right]}f\left(x\right)=6e^3;x=3\\Min_{x\in\left[0;3\right]}f\left(x\right)=-e;x=1\end{cases}\)
2. \(f\left(x\right)=x-e^{2x}\) trên đoạn \(\left[-1;0\right]\)
Ta có :
\(f'\left(x\right)=1-2e^{2x}=0\Leftrightarrow e^{2x}=\frac{1}{2}\Leftrightarrow e^{2x}=e^{\ln\frac{1}{2}}\)
\(\Leftrightarrow2x=\ln\frac{1}{2}=-\ln2\Leftrightarrow x=\frac{-\ln2}{2}\in\left[-1;0\right]\)
Mà :
\(\begin{cases}f\left(-1\right)=-1-\frac{1}{e^2}=-\frac{e^2+1}{e^2}\\f\left(-\frac{\ln2}{2}\right)=\frac{-\ln2}{2}-e^{-\ln2}=\frac{-\ln2}{2}-\frac{1}{2}=-\frac{1+\ln2}{2}\\f\left(0\right)=-1\end{cases}\)
\(\Leftrightarrow\begin{cases}Max_{x\in\left[-1;0\right]}f\left(x\right)=-\frac{1+\ln2}{2};x=-\frac{\ln2}{2}\\Min_{x\in\left[-1;0\right]}f\left(x\right)=-\frac{e^2+1}{e^2};x=-1\end{cases}\)
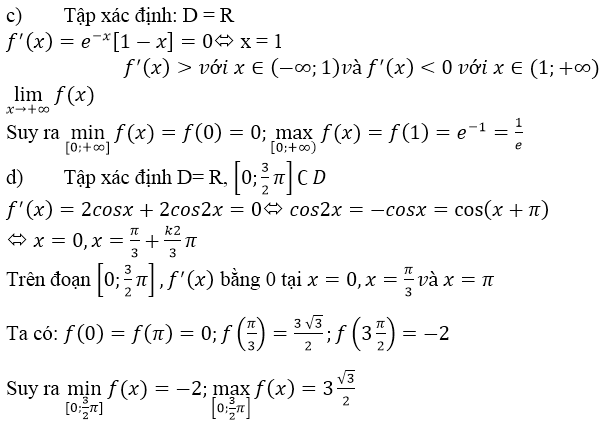
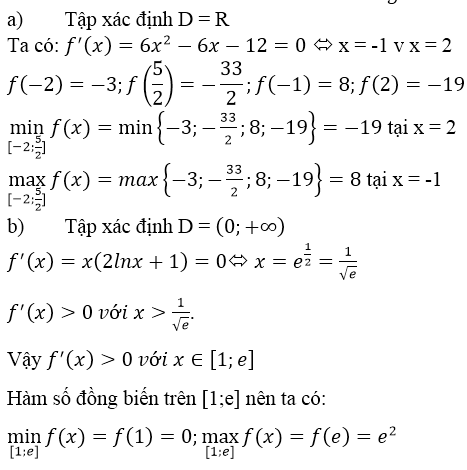
Đặt \(t=\sin^2x\Rightarrow\begin{cases}\cos^2x=1-t\\t\in\left[0;1\right]\end{cases}\) \(\Leftrightarrow f\left(x\right)=5^t+5^{1-t}=g\left(t\right);t\in\left[0;1\right]\)
Ta có : \(g'\left(t\right)=5^t\ln5-5^{1-t}\ln5=\left(5^t-5^{1-t}\right)\ln5=0\)
\(\Leftrightarrow5^t=5^{1-t}\)
\(\Leftrightarrow t=1-t\)
\(t=\frac{1}{2}\)
Mà \(\lim\limits_{x\rightarrow-\infty}g\left(t\right)=\lim\limits_{x\rightarrow-\infty}\left(5^t-5^{1-t}\right)=+\infty\)
\(\lim\limits_{x\rightarrow+\infty}g\left(t\right)=\lim\limits_{x\rightarrow+\infty}\left(5^t-5^{1-t}\right)=+\infty\)
Ta có bảng biến thiên
t g'(t) g(t) - 8 1 2 + 8 0 - + + 8 + 8 2 căn 5
\(\Rightarrow\) Min \(f\left(x\right)=2\sqrt{5}\) khi \(t=\frac{1}{2}\Leftrightarrow\sin^2x=\frac{1}{2}\Leftrightarrow\frac{1-\cos2x}{2}=\frac{1}{2}\)
\(\Leftrightarrow\cos2x=0\)
\(\Leftrightarrow x=\frac{\pi}{4}+\frac{k\pi}{2}\) \(\left(k\in Z\right)\)