K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VT
1
16 tháng 8 2023
ĐKXĐ: 4-(x-1)^2>=0
=>(x-1)^2<=4
=>-2<=x-1<=2
=>-1<=x<=3
\(\left(x-1\right)^2>=0\)
=>-(x-1)^2<=0
=>\(-\left(x-1\right)^2+4< =4\)
=>\(\sqrt{-\left(x-1\right)^2+4}< =2\)
Dấu = xảy ra khi x=1
\(\sqrt{4-\left(x-1\right)^2}>=0\forall x\) thỏa mãn ĐKXĐ
Dấu = xảy ra khi 4-(x-1)^2=0
=>(2-x+1)(2+x-1)=0
=>(3-x)(1+x)=0
=>x=3 hoặc x=-1
VT
1
16 tháng 8 2023
`\sqrt{x^2 - 2x + 4}`
`=\sqrt{(x-1)^2 + 3}`
Do `\sqrt{(x-1)^2 + 3} >=0`
`(x-1)^{2} >=0`
`=>(x-1)^{2} + 3 >=3AAx`
`=>\sqrt{(x-1)^2 + 3} >= \sqrt{3}AAx`
Dấu "=" xảy ra `<=>x-1=0`
`<=>x=1`
Vậy `min` của biểu thức là `\sqrt{3} <=>x=1`
23 tháng 6 2021
Xét A = \(3\left(\sqrt{x}-1\right)+\dfrac{12}{\sqrt{x}-1}+3\)
Áp dụng bdt Co-si, ta có:
\(3\left(\sqrt{x}-1\right)+\dfrac{12}{\sqrt{x}-1}\ge2\sqrt{3\left(\sqrt{x}-1\right)\dfrac{12}{\sqrt{x}-1}}=12\)
<=> A \(\ge15\)
Dấu"=" <=> x = 9
AH
Akai Haruma
Giáo viên
23 tháng 6 2021
Lời giải:
Vì $x>1$ nên $\sqrt{x}-1>0$
$A=3(\sqrt{x}-1)+\frac{12}{\sqrt{x}-1}+3$
Áp dụng BĐT Cô-si cho các số dương:
$3(\sqrt{x}-1)+\frac{12}{\sqrt{x}-1}\geq 2\sqrt{3.12}=12$
$\Rightarrow A\geq 12+3=15$
Vậy $A_{\min}=15$. Giá trị này đạt tại $3(\sqrt{x}-1)=\frac{12}{\sqrt{x}-1}$
$\Leftrightarrow x=9$
TT
1
14 tháng 11 2021
Ta có:
\(A=\sqrt{1-x}+\sqrt{1+x}\) \(\left(-1\le x\le1\right)\)
\(=1.\sqrt{1-x}+1.\sqrt{1+x}\)
Áp dụng BĐT Bunhiacopxki, ta có:
\(A=1.\sqrt{1-x}+1.\sqrt{1+x}\)
\(\le\sqrt{\left(1^2+1^2\right).\left(1-x+1+x\right)}=\sqrt{2.2}=2\)
Vậy \(A_{max}=2\), đạt được khi và chỉ khi \(\dfrac{1}{\sqrt{1-x}}=\dfrac{1}{\sqrt{1+x}}\Leftrightarrow1-x=1+x\Leftrightarrow x=0\)
HD
1
23 tháng 5 2021
Đk: \(x\ge0\)
\(P=\dfrac{\sqrt{x}}{x+3\sqrt{x}+4}\)
\(\Leftrightarrow x.P+\sqrt{x}\left(3P-1\right)+4P=0\) (1)
Xét P=0 <=> x=0(tm)
Xét \(P\ne0\) .Coi pt (1) là phương trình ẩn \(\sqrt{x}\)
Phương trình (1) có nghiệm không âm khi \(\Leftrightarrow\left\{{}\begin{matrix}\Delta\ge0\\S\ge0\\P\ge0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-7P^2-6P+1\ge0\\\dfrac{1-3P}{P}\ge0\\4\ge0\left(lđ\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1\le P\le\dfrac{1}{7}\\0< P\le\dfrac{1}{3}\end{matrix}\right.\) \(\Rightarrow0< P\le\dfrac{1}{7}\)
Kết hợp với P=0 \(\Rightarrow0\le P\le\dfrac{1}{7}\)
Có \(\dfrac{1}{7}>0\) => maxP=\(\dfrac{1}{7}\). Thay \(P=\dfrac{1}{7}\) vào (1) tìm được x=4 (tm)
minP=0 <=> x=0
VN
2
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 8 2021
\(P=\dfrac{2\left(x^2+2\right)+x^2-4x+4}{x^2+2}=2+\dfrac{\left(x-2\right)^2}{x^2+2}\ge2\)
\(P=\dfrac{5\left(x^2+2\right)-2x^2-4x-2}{x^2+2}=5-\dfrac{2\left(x+1\right)^2}{x^2+2}\le5\)
V
1
AH
Akai Haruma
Giáo viên
30 tháng 10 2021
Lời giải:
$y=\frac{x^2+3}{x^2-x+2}$
$\Leftrightarrow y(x^2-x+2)=x^2+3$
$\Leftrightarrow x^2(y-1)-xy+(2y-3)=0(*)$
Coi đây là pt bậc 2 ẩn $x$. Vì $y$ tồn tại nên $(*)$ luôn có nghiệm
$\Rightarrow \Delta=y^2-4(y-1)(2y-3)\geq 0$
$\Leftrightarrow -7y^2+20y-12\geq 0$
$\Leftrightarrow (7y-6)(2-y)\geq 0$
$\Leftrightarrow \frac{6}{7}\leq y\leq 2$
Vậy $y_{\min}=\frac{6}{7}; y_{\max}=2$
11 tháng 10 2021
\(y=-x^2+40x+600\)
\(=-\left(x^2-40x+400\right)+1000\)
\(-\left(x-20\right)^2+1000\le1000\)
\(y_{max}=1000\Leftrightarrow x=20\)
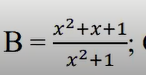
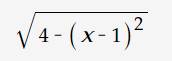
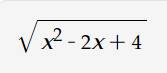
\(B=\dfrac{2x^2+2x+2}{2\left(x^2+1\right)}=\dfrac{x^2+1+x^2+2x+1}{2\left(x^2+1\right)}=\dfrac{1}{2}+\dfrac{\left(x+1\right)^2}{2\left(x^2+1\right)}\ge\dfrac{1}{2}\)
\(B=\dfrac{2x^2+2x+2}{2\left(x^2+1\right)}=\dfrac{3\left(x^2+1\right)-x^2+2x-1}{2\left(x^2+1\right)}=\dfrac{3}{2}-\dfrac{\left(x-1\right)^2}{2\left(x^2+1\right)}\le\dfrac{3}{2}\)