Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: D.
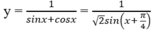
Trên khoảng (0; π /2), sin(x + π /4) ≤ 1;
Dấu "=" xảy ra ⇔ x = π /4
Suy ra giá trị nhỏ nhất của hàm số là min y = y( π /4) = 2 /2.

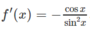
f′(x) < 0 nên và f’(x) > 0 trên ( π /2; 5 π /6] nên hàm số đạt cực tiểu tại x = π /2 và f CT = f( π /2) = 1
Mặt khác, f( π /3) = 2 3 , f(5 π /6) = 2
Vậy min f(x) = 1; max f(x) = 2

f(x) = 2sinx + sin2x trên đoạn [0; 3 π /2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 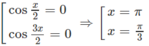
Ta có: f(0) = 0,
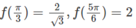
Từ đó ta có: min f(x) = −2 ; max f(x) = 3 3 /2

Lời giải:
Ta có:
\(y=\frac{k\sin x+1}{\cos x+2}\Rightarrow y\cos x+2y=k\sin x+1\)
\(\Leftrightarrow 2y-1=k\sin x-y\cos x\)
Theo BĐT Bunhiacopxky:
\((2y-1)^2=(k\sin x-y\cos x)^2\leq (k^2+y^2)(\sin ^2x+\cos ^2x)=k^2+y^2\)
\(\Leftrightarrow 4y^2-4y+1\leq k^2+y^2\)
\(\Leftrightarrow 3y^2-4y+1\leq k^2\)
\(\Leftrightarrow 3(y-\frac{2}{3})^2\leq k^2+\frac{1}{3}\)
\(\Leftrightarrow \frac{2}{3}-\sqrt{\frac{3k^2+1}{9}}\leq y\leq \frac{2}{3}+\sqrt{\frac{3k^2+1}{9}}\)
\(\Rightarrow y_{\min}=\frac{2}{3}-\sqrt{\frac{3k^2+1}{9}}\)
Để \(y_{\min}< -1\Leftrightarrow \sqrt{\frac{3k^2+1}{9}}>\frac{5}{3}\Leftrightarrow k^2>8\Leftrightarrow \left[\begin{matrix} k>2\sqrt{2}\\ k<-2\sqrt{2}\end{matrix}\right.\)

\(f\left(x\right)=\dfrac{2x-1}{x-3}=\dfrac{2\left(x-3\right)+5}{x-3}=1+\dfrac{5}{\left(x-3\right)}\)
f(x) có dạng \(y=\dfrac{5}{x}\Rightarrow\) f(x) luôn nghịch biến
Tất nhiên bạn có thể tính đạo hàm --> f(x) <0 mọi x khác -3
f(x) luôn nghich biến [0;2] < -3 thuộc nhánh Bên Phải tiệm cận đứng
\(\Rightarrow\left\{{}\begin{matrix}Max=f\left(0\right)=\dfrac{1}{3}\\Min=f\left(2\right)=-3\end{matrix}\right.\)

\(f\left(x\right)=e^{sinx}-sinx-1\)
\(\Rightarrow f'\left(x\right)=cosx.e^{sinx}-cosx=cosx\left(e^{sinx}-1\right)\)
\(f'\left(x\right)=0\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sinx=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{\pi}{2}\\x=\pi\end{matrix}\right.\)
\(f\left(0\right)=0\) ; \(f\left(\dfrac{\pi}{2}\right)=e-2\) ; \(f\left(\pi\right)=0\)
\(\Rightarrow f\left(x\right)_{min}=0\) ; \(f\left(x\right)_{max}=e-2\)
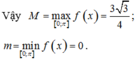


y′ = 0 ⇔ x = π
Hàm số không có giá trị nhỏ nhất. Giá trị lớn nhất của hàm số là: max y = y( π ) = −1