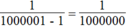Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a ) Gọi \(A=\dfrac{3x^2-x}{9x^2-6x+1}\)
Ta có : \(A=\dfrac{x\left(3x-1\right)}{\left(3x\right)^2-2.3x.1+1}=\dfrac{x\left(3x-1\right)}{\left(3x-1\right)^2}=\dfrac{x}{3x-1}\)
Thay x = - 8 và biểu thức A ta được :
\(A=\dfrac{-8}{3.\left(-8\right)-1}=\dfrac{8}{25}\)
Vậy giá trị của biểu thức A là \(\dfrac{8}{25}\) tại x = - 8
b ) Gọi \(B=\dfrac{x^2+3x+2}{x^3+2x^2-x-2}\)
Ta có \(B=\dfrac{\left(x^2+x\right)+\left(2x+2\right)}{x^2\left(x+2\right)-\left(x+2\right)}=\dfrac{x\left(x+1\right)+2\left(x+1\right)}{\left(x^2-1\right)\left(x+2\right)}=\dfrac{\left(x+2\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)\left(x+2\right)}=\dfrac{1}{x-1}\)
Thay x = 1000001 và biểu thức B ta được :
\(B=\dfrac{1}{1000001-1}=\dfrac{1}{100000}\)
Vậy giá trị của biểu thức B là \(\dfrac{1}{1000000}\) tại x = 1000001
Bài 1:
a) Để phân thức \(\frac{2}{x-3}\) có giá trị nguyên thì \(2⋮x-3\)
\(\Leftrightarrow x-3\inƯ\left(2\right)\)
\(\Leftrightarrow x-3\in\left\{1;-1;2;-2\right\}\)
\(\Leftrightarrow x\in\left\{4;2;5;1\right\}\)(tm)
Vậy: \(x\in\left\{4;2;5;1\right\}\)
b) Để phân thức \(\frac{3}{x+2}\) có giá trị nguyên thì \(3⋮x+2\)
\(\Leftrightarrow x+2\inƯ\left(3\right)\)
\(\Leftrightarrow x+2\in\left\{1;-1;3;-3\right\}\)
\(\Leftrightarrow x\in\left\{-1;-3;1;-5\right\}\)(tm)
Vậy: \(x\in\left\{-1;-3;1;-5\right\}\)
c) *Đặt phép chia:
Để phân thức \(\frac{x^4-3x^2+5}{x-3}\)nhận giá trị nguyên thì số dư chia hết cho số chia
hay \(59⋮x-3\)
\(\Leftrightarrow x-3\inƯ\left(59\right)\)
\(\Leftrightarrow x-3\in\left\{1;-1;59;-59\right\}\)
\(\Leftrightarrow x\in\left\{4;2;62;-56\right\}\)(tm)
Vậy: \(x\in\left\{4;2;62;-56\right\}\)
d)
*Đặt phép chia:
*Để phân thức \(\frac{2x^3+x^2+2x+8}{2x+1}\) nhận giá trị nguyên thì số dư chia hết cho số chia
hay \(6⋮2x+1\)
\(\Leftrightarrow2x+1\inƯ\left(6\right)\)
\(\Leftrightarrow2x+1\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
\(\Leftrightarrow2x\in\left\{0;-2;1;-3;2;-4;5;-7\right\}\)
\(\Leftrightarrow x\in\left\{0;-1;\frac{1}{2};\frac{-3}{2};1;-2;\frac{5}{2};\frac{-7}{2}\right\}\)
mà x∈Z
nên \(x\in\left\{0;-1;1;-2\right\}\)
Vậy: \(x\in\left\{0;-1;1;-2\right\}\)
Bài 2:
a) Ta có: \(\frac{3x^2-x}{9x^2-6x+1}\)
\(=\frac{x\left(3x-1\right)}{\left(3x-1\right)^2}=\frac{x}{3x-1}\)(1)
Thay x=-8 vào biểu thức (1), ta được
\(\frac{-8}{3\cdot\left(-8\right)-1}=\frac{-8}{-25}=\frac{8}{25}=0,32\)
Vậy: 0,32 là giá trị của biểu thức \(\frac{3x^2-x}{9x^2-6x+1}\) tại x=-8
b) Ta có: \(\frac{x^2+3x+2}{x^3+2x^2-x-2}\)
\(=\frac{x^2+2x+x+2}{x^2\left(x+2\right)-\left(x+2\right)}=\frac{\left(x+2\right)\left(x+1\right)}{\left(x+2\right)\left(x^2-1\right)}=\frac{x+1}{x^2-1}=\frac{x+1}{\left(x+1\right)\left(x-1\right)}=\frac{1}{x-1}\)(2)
Thay x=1000001 vào biểu thức (2), ta được
\(\frac{1}{1000001-1}=\frac{1}{1000000}\)
Vậy: \(\frac{1}{1000000}\) là giá trị của biểu thức \(\frac{x^2+3x+2}{x^3+2x^2-x-2}\) tại x=1000001
a) Để giá trị biểu thức 5 – 2x là số dương
<=> 5 – 2x > 0
<=> -2x > -5 ( Chuyển vế và đổi dấu hạng tử 5 )
\(\Leftrightarrow x< \frac{5}{2}\)( Chia cả 2 vế cho -2 < 0 ; BPT đổi chiều )
Vậy : \(x< \frac{5}{2}\)
b) Để giá trị của biểu thức x + 3 nhỏ hơn giá trị biểu thức 4x - 5 thì:
x + 3 < 4x – 5
<=< x – 4x < -3 – 5 ( chuyển vế và đổi dấu các hạng tử 4x và 3 )
<=> -3x < -8
\(\Leftrightarrow x>\frac{8}{3}\)( Chia cả hai vế cho -3 < 0, BPT đổi chiều).
Vậy : \(x>\frac{8}{3}\)
c) Để giá trị của biểu thức 2x +1 không nhỏ hơn giá trị của biểu thức x + 3 thì:
2x + 1 ≥ x + 3
<=> 2x – x ≥ 3 – 1 (chuyển vế và đổi dấu các hạng tử 1 và x).
<=> x ≥ 2.
Vậy x ≥ 2.
d) Để giá trị của biểu thức x2 + 1 không lớn hơn giá trị của biểu thức (x - 2)2 thì:
x2 + 1 ≤ (x – 2)2
<=> x2 + 1 ≤ x2 – 4x + 4
<=> x2 – x2 + 4x ≤ 4 – 1 ( chuyển vế và đổi dấu hạng tử 1; x2 và – 4x).
<=> 4x ≤ 3
\(\Leftrightarrow x\le\frac{3}{4}\)( Chia cả 2 vế cho 4 > 0 )
Vậy : \(x\le\frac{3}{4}\)
a) \(ĐKXĐ:x\ne-3;x\ne2\)
b) \(P=\frac{\left(x+2\right)\left(x-2\right)}{\left(x+3\right)\left(x-2\right)}-\frac{5}{\left(x-2\right)\left(x+3\right)}-\frac{x+3}{\left(x-2\right)\left(x+3\right)}\)
\(P=\frac{x^2-4-5-x-3}{\left(x+3\right)\left(x-2\right)}\)
\(P=\frac{x^2-x-12}{\left(x+3\right)\left(x-2\right)}\)
\(P=\frac{\left(x+3\right)\left(x-4\right)}{\left(x+3\right)\left(x-2\right)}\)
vậy \(P=\frac{x-4}{x-2}\)
\(P=\frac{-3}{4}\) \(\Leftrightarrow\frac{x-4}{x-2}=\frac{-3}{4}\)
\(\Leftrightarrow4\left(x-4\right)=-3.\left(x-2\right)\)
\(\Leftrightarrow4x-16=-3x+6\)
\(\Leftrightarrow7x=22\)
\(\Leftrightarrow x=\frac{22}{7}\)
c) \(P\in Z\Leftrightarrow\frac{x-4}{x-2}\in Z\)
\(\frac{x-2-6}{x-2}=1-\frac{6}{x-2}\in Z\)
mà \(1\in Z\Rightarrow\left(x-2\right)\inƯ\left(6\right)\in\left(\pm1;\pm2;\pm3;\pm6\right)\)
mà theo ĐKXĐ: \(\Rightarrow\in\left(\pm1;-2;3;\pm6\right)\)
thay mấy cái kia vào rồi tìm \(x\)
d) \(x^2-9=0\Rightarrow x^2=9\Rightarrow x=\pm3\)
khi \(x=3\Rightarrow P=\frac{3-4}{3-2}=-1\)
khi \(x=-3\Rightarrow P=\frac{-3-4}{-3-2}=\frac{-7}{-5}=\frac{7}{5}\)
a) ĐKXĐ: \(\hept{\begin{cases}x+2\ne0\\x^2-4\ne0\\2-x\ne0\end{cases}}\) => \(\hept{\begin{cases}x\ne-2\\x\ne\pm2\\x\ne2\end{cases}}\) => \(x\ne\pm2\)
Ta có:Q = \(\frac{x-1}{x+2}+\frac{4x+4}{x^2-4}+\frac{3}{2-x}\)
Q = \(\frac{\left(x-1\right)\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}+\frac{4x+4}{\left(x-2\right)\left(x+2\right)}-\frac{3\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\)
Q = \(\frac{x^2-2x-x+2+4x+4-3x-6}{\left(x+2\right)\left(x-2\right)}\)
Q = \(\frac{x^2-2x}{\left(x+2\right)\left(x-2\right)}=\frac{x\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}=\frac{x}{x+2}\)
b) ĐKXĐ P: x - 3 \(\ne\)0 => x \(\ne\)3
Ta có: P = 3 => \(\frac{x+2}{x-3}=3\)
=> x + 2 = 3(x - 3)
=> x + 2 = 3x - 9
=> x - 3x = -9 - 2
=> -2x = -11
=> x = 11/2 (tm)
Với x = 11/2 thay vào Q => Q = \(\frac{\frac{11}{2}}{\frac{11}{2}+2}=\frac{11}{15}\)
c) Với x \(\ne\)\(\pm\)2; x \(\ne\)3
Ta có: M = PQ = \(\frac{x+2}{x-3}\cdot\frac{x}{x+2}=\frac{x}{x-3}=\frac{x-3+3}{x-3}=1+\frac{3}{x-3}\)
Để M \(\in\)Z <=> 3 \(⋮\)x - 3
=> x - 3 \(\in\)Ư(3) = {1; -1; 3; -3}
Lập bảng:
| x - 3 | 1 | -1 | 3 | -3 |
| x | 4 | 2 (ktm) | 6 | 0 |
Vậy ...
a)\(\left(\frac{1-x^3+1-x-x}{1-x}\right):\frac{-\left(x-1\right)\left(x+1\right)}{\left(x+1\right)\left(x-1\right)^2}=\left(\frac{-x^3-2x+2}{1-x}\right)\cdot\left(1-x\right)=-x^3-2x+2\)
b) \(-\left(-1\frac{2}{3}\right)-2\cdot\left(-1\frac{2}{3}\right)+2=\frac{5}{3}+\frac{10}{3}+2=7\)
bài1 A=\(\left(\frac{3-x}{x+3}\cdot\frac{x^2+6x+9}{x^2-9}+\frac{x}{x+3}\right):\frac{3x^2}{x+3}\)
=\(\left(-\frac{x-3\cdot\left(x+3\right)^2}{\left(x+3\right)^2\cdot\left(x-3\right)}+\frac{x}{x+3}\right):\frac{3x^2}{x+3}\)
=\(-\frac{x}{x+3}\cdot\frac{x+3}{3x^2}=\frac{-1}{3x}\)
b) thế \(x=-\frac{1}{2}\)vào biểu thức A
\(-\frac{1}{3\cdot\left(-\frac{1}{2}\right)}=\frac{2}{3}\)
c) A=\(-\frac{1}{3x}< 0\)
VÌ (-1) <0 nên 3x>0
x >0
Ta có: x 3 + 2 x 2 - x - 2 = x 2 x + 2 - x + 2 = x 2 - 1 . x + 2 = x + 1 x - 1 x + 2
Do đó, để x 3 + 2 x 2 - x - 2 ≠ 0 khi (x + 2)(x – 1)(x + 1) ≠ 0 ⇒ x ≠ - 2 và x ≠ ± 1
Ta có: x = 1000001 thỏa mãn điều kiện.
Thay x = 1000001 vào biểu thức ta được: