Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

nửa chu vi hình chữ nhật : 56/2=28cm
gọi x là chiều rộng của hình chữ nhật
chiều dài HCN:28-x(m)
chiều rộng sau khi giảm:x-2(m)
chiều dài sau khi tăng: 28-x+4=32-x(m)
theo đề bài ta có phương trình:
x.(28-x)=8-(x-2)(32-x)
<=>28x-x2=72-34x+x2
<=>62x-2x2-72=0
<=>x=1,21(m)
chiều dài : 28-1,21=26,79(m)
Nếu đúng thì T I C K cho mình nhé
Thống nhất đơn vị đo là m nhá -.-
Nửa chu vi miếng đất : 56 : 2 = 28m
Gọi chiều dài miếng đất là x ( m , \(x\inℕ^∗,x< 28\))
=> Chiều rộng miếng đất = 28 - x ( m )
Giảm chiều rộng 2m và tăng chiều dài 4m
=>\(\hept{\begin{cases}\text{ Chiều rộng mới = 28 - x - 2 = 26 - x ( m )}\\\text{Chiều dài mới = x + 4 ( m )}\end{cases}}\)
Diện tích ban đầu = x( 28 - x ) ( m2 )
Diện tích sau khi thay đổi = ( x + 4 )( 26 - x ) ( m2 )
Khi đó diện tích tăng thêm 8m2
=> Ta có phương trình : x( 28 - x ) + 8 = ( x + 4 )( 26 - x )
<=> 28x - x2 + 8 = 22x - x2 + 104
<=> 28x - x2 - 22x + x2 = 104 - 8
<=> 6x = 96
<=> x = 16 ( tmđk )
Vậy chiều dài miếng đất là 16m
chiều rộng miếng đất = 28 - 16 = 12m

Gọi chiều dài chiều rộng miếng đất lần lượt là a ; b ( a > b > 0 )
Theo bài ra ta có hệ \(\left\{{}\begin{matrix}b=\dfrac{3}{5}a\\2\left(a+b\right)=32\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{5}a-b=0\\a+b=16\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=10\\b=6\end{matrix}\right.\left(tm\right)\)
Diện tích miếng đất là ab = 60 m2
Nửa chu vi miếng đất:
32:2=16(m)
Tổng số phần bằng nhau:
3+5=8(phần)
Chiều dài miếng đất:
16:8x 5= 10(m)
Chiều rộng miếng đất:
16-10=6(m)
Diện tích miếng đất:
10 x 6= 60(m2)

Gọi độ dài của mỗi cạnh của hình chữ nhật là x, và y (m)
Đk : x, y > 0
Tổng độ dài 2 cạnh là:
x + y = 24/2
=> x + y = 12 (1)
Nếu tăng độ dài 1 cạnh (x) lên 2m và giảm cạnh còn lại (y) 1m thì diện tích mảnh đất tăng thêm 1m², ta có:
(x + 2).(y - 1) = xy + 1
=> xy - x + 2y - 2 = xy + 1
=> 2y - x = 3 (2)
Từ (1) và (2), ta có hệ phương trình:
{ x + y = 12
2y - x = 3
=> { x = 12 - y
2y - x + x + y = 3 + 12
=> { x = 12 - y
3y = 15
=> { x = 7 (tm)
y = 5 (tm)
Vậy độ dài các cạnh của hình chữ nhật là 7m và 5m.

Câu hỏi của Huy đức - Toán lớp 9 - Học toán với OnlineMath

Gọi chiều dài chiều rộng ban đầu là a,b
Sau khi làm lối đi thì chiều dài chiều rộng là (a -4), (b - 4)
Theo đề bài ta có
\(\hept{\begin{cases}2\left(a+b\right)=280\\\left(a-4\right)\left(b-4\right)=\:4256\end{cases}}\)
=> a = 80; b = 60

Gọi chiều dài miếng đất hình chữ nhật đó là : \(a\left(m/0< a< 25\right)\)
Do chiều rộng bằng 2 lần chiều dài nên chiều rộng là \(2a\left(m\right)\)
Ta có phương trình :
\(\left(a+2a\right)\times2=50\)
\(\Leftrightarrow3a=25\)
\(\Leftrightarrow a=\frac{25}{3}\left(tm\right)\)
Vậy chiều dài là \(\frac{25}{3}\left(m\right)\)
Chiều rộng là \(2\times\frac{25}{3}=\frac{50}{3}\left(m\right)\)
Diện tích miếng đất là : \(\frac{25}{3}\times\frac{50}{3}=\frac{1250}{9}\left(m^2\right)\)
Vậy ....

Gọi a, b lần lượt là chiều dài , chiều rộng của mảnh vườn.(a,b ϵ N*)
Ta có hệ phương trình: a + b = 280 + 2 = 282
ab = 4256
=> a = 266, b = 16
Vậy chiều dài của mảnh vườn là 266 cm, chiều rộng là 16 cm.
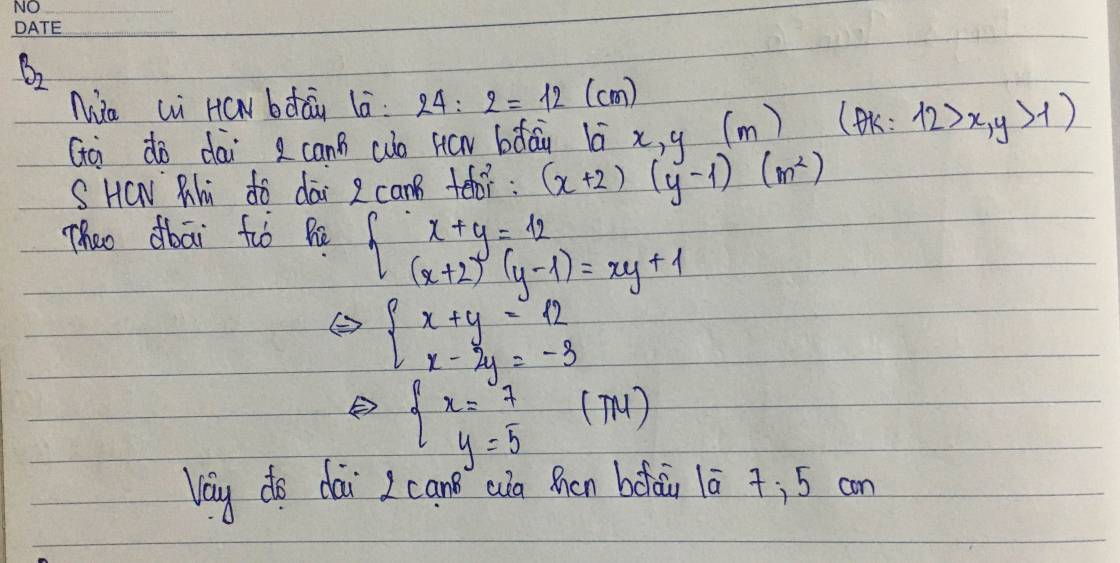
nửa chu vi: 280:2=140
gọi chiều dài của hcn là :x => chiều rộng là: 140-x
vì diện tích là 4800 nên ta có pt: \(x\left(140-x\right)=4800\Leftrightarrow x^2-140x+4800=0\Leftrightarrow x^2-80x-60x+4800=0\Leftrightarrow\left(x-80\right)\left(x-60\right)=0\)
=> chiều dài là 80m thì rộng là 60m và ngược lại