
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a) phân thức xác định khi \(x^3+8\ne0\Leftrightarrow x^3\ne-8\Leftrightarrow x\ne-2\)
b)\(\frac{2x^2-4x+8}{x^3+8}=\frac{2\left(x^2-2x+4\right)}{\left(x+2\right)\left(x^2-2x+4\right)}=\frac{2}{x+2}\)
c) \(\frac{2}{x+2}=\frac{2}{2+2}=\frac{2}{4}=\frac{1}{2}\)
d)\(\frac{2}{x+2}=2\Leftrightarrow x+2=1\Leftrightarrow x=-1\)

a) ĐKXĐ: : x ≠ 1 và x ≠ -1.
b) Quy đồng và khử mẫu ta được PT: x(x + 1) = (x – 1)(x +4)
⇔ x2 +x = x2 +4x– x -4
⇔ x – 4x +x = -4 -2x = -4 x = 2(thỏa mãn ĐKXĐ)
Vậy PT có tập nghiệm S = {2}

a) x(x-y) + y(x+y) = x^2 - xy + yx + y^2 = x^2 + y^2 = (-6)^2 + 8^2 = 100
b) x(x^2 - y ) - x^2( x + y ) + y(x^2 - x )
= x^3 - xy - x^3 -x^2y+yx^2 - xy
= ( x^3 - x^3 ) + ( x^2 y - x^2 y ) + ( -xy - xy )
= -2xy
Bạn kiểm tra lại đề nhé!

\(A\)xác định
\(\Leftrightarrow3x^2+4x-15\ne0\)
\(\Leftrightarrow\left(3x^2+9x\right)-\left(5x+15\right)\ne0\)
\(\Leftrightarrow3x\left(x+3\right)-5\left(x+3\right)\ne0\)
\(\Leftrightarrow\left(x+3\right)\left(3x-5\right)\ne0\)
\(\Leftrightarrow\orbr{\begin{cases}x\ne3\\x\ne\frac{5}{3}\end{cases}}\)
Vậy với \(\orbr{\begin{cases}x\ne3\\x\ne\frac{5}{3}\end{cases}}\)thì \(A\)xác định
Tham khảo nhé~
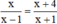



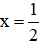 và y = –100;
và y = –100;
Phương trình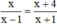 xác định
xác định
Vậy ĐKXĐ của phương trình là x ≠ ±1.