PN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
8 tháng 4 2019
Ta có hai tam giác ABC và tam giác NPM có B C = P M , B ^ = P ^ = 90 0 mà BC, PM là hai cạnh góc vuông của tam giác ABC và NPM nên để hai tam giác bằng nhau theo trường hợp cạnh huyền – cạnh góc vuông thì ta cần thêm điều kiện CA = MN
Đáp án C
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
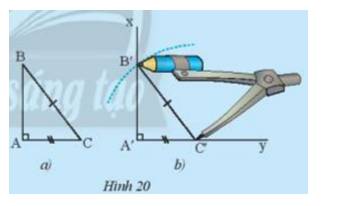
Ta nhận thấy 2 hình bằng nhau (chồng lên nhau vì vừa khít)
PT
Tính cạnh góc vuông của một tam giác vuông biết cạnh huyền bằng 13 cm, cạnh góc vuông kia bằng 12 cm
1
CM
7 tháng 5 2019
Giả sử ∆ABC có ∠A =90o, BC = 13 cm, AC = 12cm
Theo định lý pitago ta có: BC2 = AB2 + AC2
Suy ra: AB2=BC2-AC2=132-122=25
Vậy AB = 5 cm
SM
5 tháng 9 2018
Gọi độ dài cạnh góc vuông của tam giác đó là a
Theo định lí Pitago :
a2 + a2 = 492
=> 2a2 = 2401
=> a2 = 2401 : 2 = 1200.5
=> a = \(\frac{49\sqrt{2}}{2}\)
5 tháng 9 2018
ta có: tam giác ABC vuông cân tại A
=> AB = AC ( định lí) => AB2 = AC2
Xét tam giác ABC vuông tại A
=> AB2 + AC2 = 492 ( py-ta-go)
AB2 + AB2 = 492
2.AB2 = 492
AB2 = 1200,5
\(\Rightarrow AB=\sqrt{1200,5}cm\)
=> \(AB=AC=\sqrt{1200,5}cm\)
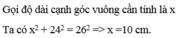
Để 1 cạnh góc vuông bằng 1 nửa cạnh huyền
<=> Góc đối diện với cạnh góc vuông đó=30 độ