
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét tam giác ABC vuông tại A:
\(BC^2=AB^2+AC^2\left(Pytago\right)\)
\(\Rightarrow AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AB.AC=\dfrac{1}{2}.3.4=6\left(cm^2\right)\)

![]()
Suy ra: tam giác ABC vuông tại A.
Diện tích tam giác ABC là:
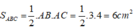
*Gọi tam giác ABC đồng dạng với tam giác MNP theo tỉ số k
Suy ra:
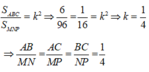
Thay số
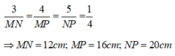
Chọn đáp án B

a: XétΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
DO đó: ΔABC\(\sim\)ΔHBA
b: Ta có: ΔABC\(\sim\)ΔHBA
nên BA/BH=BC/BA
hay \(BA^2=BH\cdot BC\)

Kẻ \(AH\perp BC\left(H\in BC\right)\)
Ta có: \(AB^2+AC^2=BC^2\left(3^2+4^2=5^2\right)\Rightarrow\Delta ABC\) vuông tại A
\(AH.BC=AB.AC\left(=2S_{ABC}\right)\Rightarrow AH.5=3.4\Rightarrow AH=2,4\left(cm\right)\)
AD là tia p/g của \(\widehat{BAC}\left(D\in BC\right)\Rightarrow\)\(\frac{DB}{DC}=\frac{AB}{AC}=\frac{3}{4}\)
\(\Rightarrow\frac{DB}{DB+DC}=\frac{3}{3+4}\Rightarrow\frac{DB}{BC}=\frac{3}{7}\Rightarrow\frac{DB}{5}=\frac{3}{7}\Rightarrow DB=\frac{15}{7}\left(cm\right)\)
\(BM=\frac{1}{2}BC=\frac{1}{2}.5=\frac{5}{2}\left(cm\right)\)
Do đó: \(DM=BM-BD=\frac{5}{2}-\frac{15}{7}=\frac{5}{14}\left(cm\right)\)
Vậy \(S_{ADM}=\frac{1}{2}AH.DM=\frac{1}{2}.2,4.\frac{5}{14}=\frac{3}{7}\left(cm^2\right)\)

\(\text{Diện tích tam giác là}:S=\dfrac{AH.BC}{2}=\dfrac{3.4}{2}=\dfrac{12}{2}=6\left(cm^2\right)\)

Kẻ AH vuông góc vs BC
=> dt tam giác ABC la: (AH.BC)/2
=>để dt tam giác ABC lớn nhất thi AH lớn nhất
Có AH nhỏ hơn hoặc = AB(định lý đương vuông góc, đương xiên)
vậy AH lớn nhất khi AH=AB=2cm
dt lớn nhất của tam giác ABC la :(AH.BC)/2=(AB.BC)/2=(2*5)/2=5

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: BC=căn 3^2+4^2=5cm
AH=3*4/5=2,4cm
c: Xét ΔAHB vuông tại H và ΔCHA vuông tại H có
góc HAB=góc HCA
=>ΔAHB đồng dạng với ΔCHA
=>S AHB/S CHA=(AB/CA)^2=9/16

a: \(S_{ABC}=3\cdot\dfrac{4}{2}=6\left(cm^2\right)\)
b: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
MB/AB=MC/AC
=>MB/3=MC/4=(MB+MC)/(3+4)=5/7
=>MB=15/7cm
Ta có: S A B C = 1 2 A H . B C
Mà AH £ AB
⇒ S A B C ≤ 1 2 A B . B C = 6.
Vậy diện tích lớn nhất của DABC là 6cm2.
Dấu "=" xảy ra Û AH º BC Û DABC vuông tại B