Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đường thẳng ![]() có
có ![]()
Đường thẳng cần tìm có ![]() và đi qua điểm M( -2; 3) nên có phương trình tham số là
và đi qua điểm M( -2; 3) nên có phương trình tham số là 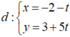 .
.
Chọn A.

PTHĐGD là:
(2m-2)x+1-2m=1/2(1-m)x+3/2(1-m)
=>\(\Leftrightarrow x\left(2m-2-\dfrac{1}{2\left(1-m\right)}\right)=\dfrac{3}{2\left(1-m\right)}-1+2m\)
\(\Leftrightarrow x\cdot\left(\dfrac{4\left(m-1\right)\left(m-1\right)+1}{2\left(m-1\right)}\right)=\dfrac{3+2\left(1-m\right)\left(-1+2m\right)}{2\left(1-m\right)}\)
\(\Leftrightarrow x\cdot\dfrac{4m^2-8m+4+1}{2\left(m-1\right)}=\dfrac{3+\left(2-2m\right)\left(2m-1\right)}{2\left(1-m\right)}\)
\(\Leftrightarrow x=\dfrac{3-4m-2-4m^2+2m}{4m^2-8m+4}=\dfrac{-4m^2-2m+1}{4m^2-8m+4}\)
=>\(y=\left(2m-2\right)\cdot\dfrac{-4m^2-2m+1}{4\left(m-1\right)^2}+1-2m\)
\(=\dfrac{2\left(m-1\right)\left(-4m^2-2m+1\right)}{4\left(m-1\right)^2}+1-2m\)
\(=\dfrac{-4m^2-2m+1}{2\left(m-1\right)}+\left(-2m+1\right)\)
\(=\dfrac{-4m^2-2m+1+\left(-2m+1\right)\cdot\left(2m-2\right)}{2\left(m-1\right)}\)
\(=\dfrac{-4m^2-2m+1-4m^2+4m-2m+2}{2\left(m-1\right)}\)
\(=\dfrac{-8m^2+3}{2\left(m-1\right)}\)

Do 2 đường thẳng d và d’ vuông góc với nhau nên d có véc tơ chỉ phương
![]() .
.
Mà d đi qua điểm M( -2; 3) nên d có phương trình tham số là:
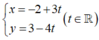
Chọn B.

a) Thay x=-1 và y=4 vào (d), ta được:
\(3m\cdot\left(-1\right)+m-2=4\)
\(\Leftrightarrow-2m=6\)
hay m=-3
b) Để (d)//(Δ) thì \(\left\{{}\begin{matrix}3m=6\\m-2\ne-1\end{matrix}\right.\Leftrightarrow m=2\)

Đáp án A
Do 2 đường thẳng d và (d’) vuông góc với nhau nên VTCP của đường thẳng này là VTPT của đường thẳng kia và ngược lại.
Mà đường thẳng (d’) có VTPT là n → ( 1 ; 6 ) n ê n u → ( 1 ; 6 ) là VTCP của đường thẳng (d) .
Khi đó phương trình tham số của đường thẳng (d) cần tìm là: