
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,x^2-\left(2m-3\right)x+m^2=0-vô-ngo\)
\(\Leftrightarrow\Delta< 0\Leftrightarrow[-\left(2m-3\right)]^2-4m^2< 0\Leftrightarrow m>\dfrac{3}{4}\)
\(b,\left(m-1\right)x^2-2mx+m-2=0\)
\(m-1=0\Leftrightarrow m=1\Rightarrow-2x-1=0\Leftrightarrow x=-0,5\left(ktm\right)\)
\(m-1\ne0\Leftrightarrow m\ne1\Rightarrow\Delta'< 0\Leftrightarrow\left(-m\right)^2-\left(m-2\right)\left(m-1\right)< 0\Leftrightarrow m< \dfrac{2}{3}\)
\(c,\left(2-m\right)x^2-2\left(m+1\right)x+4-m=0\)
\(2-m=0\Leftrightarrow m=2\Rightarrow-6x+2=0\Leftrightarrow x=\dfrac{1}{3}\left(ktm\right)\)
\(2-m\ne0\Leftrightarrow m\ne2\Rightarrow\Delta'< 0\Leftrightarrow[-\left(m+1\right)]^2-\left(4-m\right)\left(2-m\right)< 0\Leftrightarrow m< \dfrac{7}{8}\)

f(x) = (m-2) x 2 - 2mx + m + 1 > 0 (*)
Với m = 2 thì bất phương trình (*) trở thành:
f(x) = -4x + 3 > 0 ⇔ x < 3/4
Vậy với m = 2 thì bất phương trình (*) có nghiệm x < 3/4 nên m = 2 (loại)
Với m ≠ 2 thì bất phương trình (*) vô nghiệm khi và chỉ khi
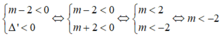
Vậy với m < -2 thì bất phương trình (*) vô nghiệm

mx²+2(m-1)x+4 ≥0
bpt trên vô nghiệm <=>mx²+2(m-1)x+4 <0
a=m\(\ne0\)
\(\Delta'=\left(m-1\right)^2-m.4\)
\(=m^2-2m+1-4m\)
\(=m^2-6m+1\)
\(=\left(m-3-2\sqrt{2}\right)\left(m-3+2\sqrt{2}\right)\)
bpt vô nghiệm <=>\(\left\{{}\begin{matrix}a< 0\\\Delta'< 0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}m< 0\\\left(m-3-2\sqrt{2}\right)\left(m-3+2\sqrt{2}\right)< 0\end{matrix}\right.\)
<=>\(\left\{{}\begin{matrix}m< 0\\3-2\sqrt{2}< m< 3+2\sqrt{2}\end{matrix}\right.\)
=> không có m để bất phương trình vô nghiệm

BPT đã cho vô nghiệm khi và chỉ khi: \(x^2-mx+m+3\ge0\) nghiệm đúng với mọi x
\(\Rightarrow\left\{{}\begin{matrix}a=1>0\\\Delta=m^2-4\left(m+3\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow m^2-4m-12\le0\)
\(\Rightarrow-2\le m\le6\)

\(x^2+2mx-2m+3>=0\)(1)
\(\text{Δ}=\left(2m\right)^2-4\cdot1\cdot\left(-2m+3\right)\)
\(=4m^2+8m-12\)
\(=4\left(m^2+2m-3\right)=4\left(m+3\right)\left(m-1\right)\)
Để bất phương trình (1) đúng với mọi x thuộc R thì \(\left\{{}\begin{matrix}\text{Δ}< =0\\a>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4\left(m+3\right)\left(m-1\right)< =0\\1>0\end{matrix}\right.\)
=>\(\left(m+3\right)\left(m-1\right)< =0\)
TH1: \(\left\{{}\begin{matrix}m+3>0\\m-1< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>-3\\m< 1\end{matrix}\right.\)
=>-3<m<1
TH2: \(\left\{{}\begin{matrix}m+3< 0\\m-1>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m< -3\\m>1\end{matrix}\right.\)
=>\(m\in\varnothing\)

\(mx^2-2\left(m+2\right)x+2m-1< 0\)
\(< =>mx^2-2\left(m+2\right)x+2m-1\ge0\)
\(a=m\ne0\)
\(\Delta=\left(2m+2\right)^2-4m\left(2m-1\right)\)
\(\Delta=4m^2+8m+4-8m^2+4m\)
\(\Delta=12m-4m^2+4\)
\(< =>\hept{\begin{cases}a>0\\\Delta\le0\end{cases}\hept{\begin{cases}m>0\\12m-4m^2+4\le0\end{cases}\hept{\begin{cases}m>0\\m=\left[\frac{3-\sqrt{13}}{2};\frac{3+\sqrt{13}}{2}\right]\end{cases}}}}\)
\(< =>m=(0;\frac{3+\sqrt{13}}{2}]\)
vậy m vô số nghiệm để bpt vô nghiệm

Với \(m=0\) BPT vô nghiệm (thỏa mãn)
Với \(m\ne0\) BPT vô nghiệm khi: \(mx^2-2mx+2m+1>0\) nghiệm đúng với mọi x
\(\Rightarrow\left\{{}\begin{matrix}a=m>0\\\Delta'=m^2-m\left(2m+1\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\m^2+m>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>0\\\left[{}\begin{matrix}m>0\\m< -1\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow m>0\)
Kết hợp lại ta được: \(m\ge0\) thì BPT đã cho vô nghiệm
https://hoc24.vn/cau-hoi/.5065181574698
Thầy oi cíu em :<