NS
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 2 2022
gọi (a+b)=x,c=y
=>\(\left[\left(a+b\right)+c\right]^2=\left(x+y\right)^2\ge4xy=4\left(a+b\right)c\)
15 tháng 2 2022
cái của bạn hơi sai sai phải là (b+c)4(b+c).a\(\ge\)16abc
dấu bằng xảy ra khi b=c=\(\dfrac{a}{2}\)
QT
Quoc Tran Anh Le
Giáo viên
17 tháng 7 2021
À mà kì lần trước, trong vòng 3, bạn đạt điểm cao nhất (quán quân) đạt được 71.25 điểm. Liệu năm nay các bạn có phá được kỉ lục này?
Ai tham gia cũng có thưởng á, cố lên các bạn vòng 3 ơi :))
SB
giúp tôi check đáp án câu này với
1
28 tháng 9 2021
\(3x-2\sqrt{3x-2}=1\left(đk:x\ge\dfrac{2}{3}\right)\)
\(\Leftrightarrow2\sqrt{3x-2}=3x-1\)
\(\Leftrightarrow4\left(3x-2\right)=9x^2-6x+1\)
\(\Leftrightarrow9x^2-18x+9=0\)
\(\Leftrightarrow9\left(x-1\right)^2=0\Leftrightarrow x=1\left(tm\right)\)
cho em xin đáp án chi tiết câu b
AT
10 tháng 1 2022
a)
M = ( 1 + \(\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\))(1 - \(\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\))
= (\(\dfrac{\sqrt{a}+1}{\sqrt{a}+1}\)+ \(\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\))(\(\dfrac{\sqrt{a}-1}{\sqrt{a}-1}\)- \(\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\))
= \(\dfrac{\sqrt{a}+1+a+\sqrt{a}}{\sqrt{a}+1}\) ✖\(\dfrac{\sqrt{a}-1-a+\sqrt{a}}{\sqrt{a}-1}\)
= \(\dfrac{a+2\sqrt{a}+1}{\sqrt{a}+1}\)✖\(\dfrac{-\left(a-2\sqrt{a}+1\right)}{\sqrt{a}-1}\)
= \(\dfrac{\left(\sqrt{a}+1\right)^2}{\sqrt{a}+1}\)✖\(\dfrac{-\left(\sqrt{a}-1\right)^2}{\left(\sqrt{a}-1\right)}\) = (\(\sqrt{a}+1\)) ✖ -(\(\sqrt{a}-1\)) = - (\(\sqrt{a}+1\)) ✖ (\(\sqrt{a}-1\)) = -(a-1) = 1-a
b)
M = 0 ↔ 1 -a = 0 ↔a = 1
Vậy với a = 1 thì M = 0
13 tháng 1
Câu 2: \(\sqrt{x-2}=2\left(ĐKXĐ:x>=2\right)\)
=>x-2=4
=>x=6(nhận)
=>x2=62=36
=>Chọn D
Câu 4:
\(\sqrt{a+b-9}+\sqrt{a+b+1}\)
\(=\dfrac{\left(a+b-9\right)-\left(a+b+1\right)}{\sqrt{a+b-9}-\sqrt{a+b+1}}\)
\(=\dfrac{-10}{-2}=5\)
=>Chọn D
PT
1
CM
27 tháng 6 2017
Chọn đáp án C
- Ta có 2 < 3 ⇒ Đáp án A sai.
- Ta có 5 > 4 ⇒ Đáp án B sai.
- Ta có 7 < 9 ⇒ Đáp án C đúng.
- Theo định nghĩa không tồn tại căn bậc hai của số âm. Đáp án D sai
20 tháng 2 2022
Chọn C
Vì x+2y=3 thì 2y=3-x
=>y=3/2-1/2x
Do đó: Phương trình có vô số nghiệm
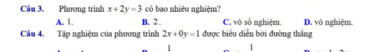
\(\text{Đề sai rồi bạn ơi}\)