Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(f'\left( x \right) = - \frac{1}{{{{\sin }^2}x}} \Rightarrow f'\left( { - \frac{\pi }{3}} \right) = - \frac{1}{{{{\sin }^2}\left( { - \frac{\pi }{3}} \right)}} = - \frac{4}{3}\)

\(f'\left( x \right) = \frac{1}{{{{\cos }^2}x}} \Rightarrow f'\left( { - \frac{\pi }{6}} \right) = \frac{1}{{{{\cos }^2}\left( { - \frac{\pi }{6}} \right)}} = \frac{4}{3}\)

a) \(y' = \left( {{x^3} - 3{x^2} + 4} \right)' = 3{x^2} - 6x\), \(y'\left( 2 \right) = {3.2^2} - 6.2 = 0\)
Thay \({x_0} = 2\) vào phương trình \(y = {x^3} - 3{x^2} + 4\) ta được: \(y = {2^3} - {3.2^2} + 4 = 0\)
Ta có phương trình tiếp tuyến của đồ thị hàm số: \(y = 0.(x - 2) + 0 = 0\)
Vậy phương trình tiếp tuyến của đồ thị hàm số là y = 0
b) \(y' = \left( {\ln x} \right)' = \frac{1}{x}\), \(y'(e) = \frac{1}{e}\)
Thay \({x_0} = e\) vào phương trình \(y = \ln x\) ta được: \(y = \ln e = 1\)
Ta có phương trình tiếp tuyến của đồ thị hàm số: \(y = \frac{1}{e}.\left( {x - e} \right) + 1 = \frac{1}{e}x - 1 + 1 = \frac{1}{e}x\)
Vậy phương trình tiếp tuyến của đồ thị hàm số là: \(y = \frac{1}{e}x\)
c) \(y' = \left( {{e^x}} \right)' = {e^x},\,\,y'(0) = {e^0} = 1\)
Thay \({x_0} = 0\) vào phương trình \(y = {e^x}\) ta được: \(y = {e^0} = 1\)
Ta có phương trình tiếp tuyến của đồ thị hàm số: \(y = 1.\left( {x - 0} \right) + 1 = x + 1\)
Vậy phương trình tiếp tuyến của đồ thị hàm số là: \(y = x + 1\)

\(f'\left(x\right)=\dfrac{1}{x\cdot ln10}\)
=>\(f'\left(\dfrac{1}{2}\right)=\dfrac{1}{\dfrac{1}{2}\cdot ln10}=\dfrac{2}{ln10}\)

a. \(y'\left(x_0\right)=-2x_0+3\)
b. phương trình tiếp tuyến tại x0 =2 là
\(y=y'\left(x_0\right)\left(x-x_0\right)+y_0=-\left(x-2\right)+0\text{ hay }y=-x+2\)
c.\(y_0=0\Rightarrow\orbr{\begin{cases}x_0=1\\x_0=2\end{cases}\Rightarrow PTTT\orbr{\begin{cases}y=x-1\\y=-x+2\end{cases}}}\)
d. vì tiếp tuyến vuông góc với đường thẳng có hệ số góc bằng 1 nên tiếp tuyến có hệ số góc = -1
hay \(-2x_0+3=-1\Leftrightarrow x_0=2\Rightarrow PTTT:y=-x+2\)

f(x) = sin x
=> f'(x) = cos x
\(f'\left(\dfrac{\pi}{2}\right)=cos\left(\dfrac{\pi}{2}\right)=0\)

1) \(f\left(x\right)=2x-5\)
\(f'\left(x\right)=2\)
\(\Rightarrow f'\left(4\right)=2\)
2) \(y=x^2-3\sqrt[]{x}+\dfrac{1}{x}\)
\(\Rightarrow y'=2x-\dfrac{3}{2\sqrt[]{x}}-\dfrac{1}{x^2}\)
3) \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt[]{x}\)
\(\Rightarrow f'\left(x\right)=\dfrac{1.\left(x+3\right)-1.\left(x+9\right)}{\left(x-3\right)^2}+\dfrac{4}{2\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{x+3-x-9}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=\dfrac{12}{\left(x-3\right)^2}+\dfrac{2}{\sqrt[]{x}}\)
\(\Rightarrow f'\left(x\right)=2\left[\dfrac{6}{\left(x-3\right)^2}+\dfrac{1}{\sqrt[]{x}}\right]\)
\(\Rightarrow f'\left(1\right)=2\left[\dfrac{6}{\left(1-3\right)^2}+\dfrac{1}{\sqrt[]{1}}\right]=2\left(\dfrac{3}{2}+1\right)=2.\dfrac{5}{2}=5\)
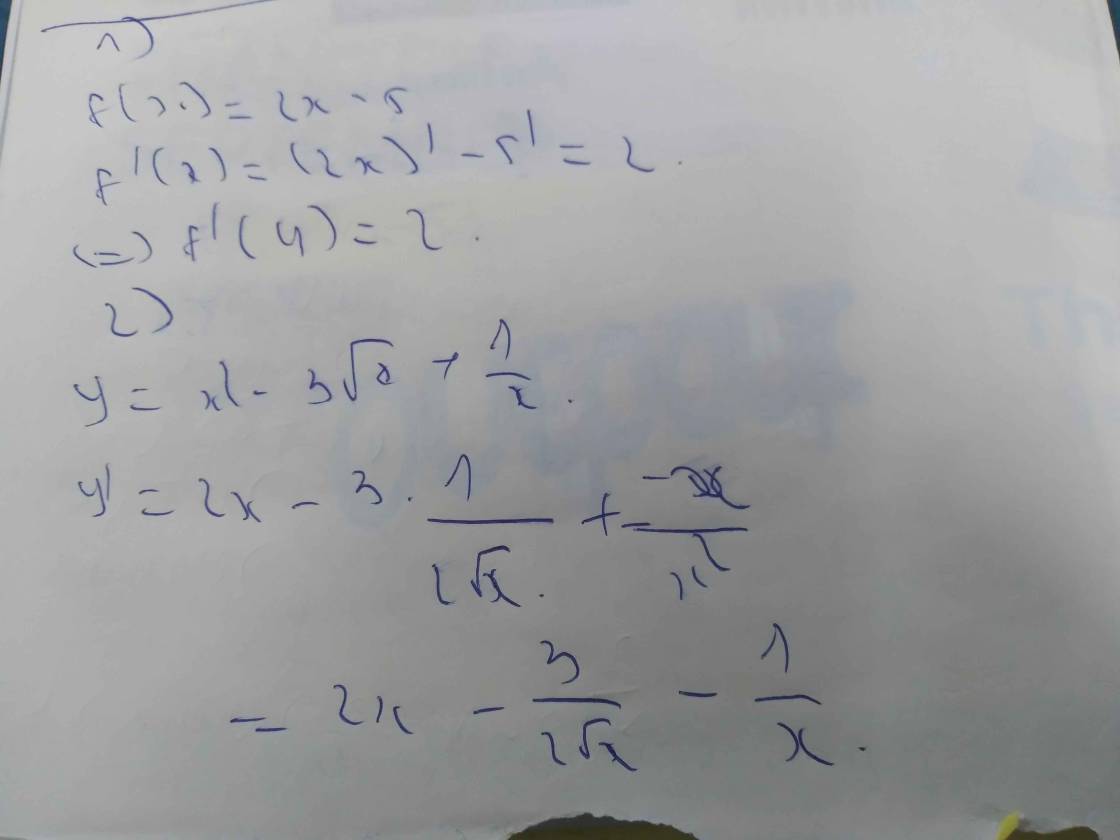

a,
\(y' = 6x - 4 \Rightarrow y'' = 6\)
Tại \({x_0} = - 2 \Rightarrow y''( - 2) = 6\)
b,
\(\begin{array}{l}y' = \frac{2}{{\left( {2x + 1} \right)\ln 3}}\\ \Rightarrow y'' = \left( {2.\frac{1}{{\left( {\left( {2x + 1} \right)\ln 3} \right)}}} \right)' = - 2.\frac{{\left( {\left( {2x + 1} \right)\ln 3} \right)'}}{{{{\left( {\left( {2x + 1} \right)\ln 3} \right)}^2}}}\\ = - 2\frac{{2\ln 3}}{{{{\left( {\left( {2x + 1} \right)\ln 3} \right)}^2}}} = \frac{{ - 4\ln 3}}{{{{\left( {\left( {2x + 1} \right)\ln 3} \right)}^2}}}\end{array}\)
Tại \({x_0} = 3 \Rightarrow y''(3) = \frac{{ - 4\ln 3}}{{{{\left( {\left( {2.3 + 1} \right)\ln 3} \right)}^2}}} = \frac{{ - 4\ln 3}}{{{{\left( {7\ln 3} \right)}^2}}} = \frac{{ - 4}}{{49\ln 3}}\)
c, \(y' = 4{e^{4x + 3}} \Rightarrow y'' = 16{e^{4x + 3}}\)
Tại \({x_0} = 1 \Rightarrow y''(1) = 16.{e^{4.1 + 3}} = 16.{e^7}\)
d,
\(y' = 2\cos \left( {2x + \frac{\pi }{3}} \right) \Rightarrow y'' = - 4\sin \left( {2x + \frac{\pi }{3}} \right)\)
Tại \({x_0} = \frac{\pi }{6} \Rightarrow y''\left( {\frac{\pi }{6}} \right) = - 4\sin \left( {2.\frac{\pi }{6} + \frac{\pi }{3}} \right) = - 2\sqrt 3 \)
e,
\(y' = - 3.\sin \left( {3x - \frac{\pi }{6}} \right) \Rightarrow y'' = - 9.\cos \left( {3x - \frac{\pi }{6}} \right)\)
Tại \({x_0} = 0 \Rightarrow y''(0) = - 9.\cos \left( {3.0 - \frac{\pi }{6}} \right) = \frac{{ - 9\sqrt 3 }}{2}\)