
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

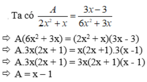

1. \(\left(x+1\right)^3-125\)
\(=\left(x+1\right)^3-5^3\)
\(=\left(x+1-5\right).\left[\left(x+1\right)^2+\left(x+1\right).5+5^2\right]\)
2. \(\left(x+4\right)^3-64\)
\(=\left(x+4\right)^3-4^3\)
\(=\left(x+4-4\right).\left[\left(x+4\right)^2+\left(x+4\right).4+4^2\right]\)
3. \(x^3-\left(y-1\right)^3\)
\(=(x^3-y+1).\left[\left(x^2\right)+x.\left(y+1\right)+\left(y+1\right)^2\right]\)
\(\)4. \(\left(a+b\right)^3-c^3\)
\(=\left[\left(a+b\right)-c\right].\left[\left(a+b\right)^2+\left(a+b\right).c+c^2\right]\)
5. \(125-\left(x+2\right)^3\)
\(=5^3-\left(x+2\right)^3\)
\(=\left(5-x-2\right).\left[5^2+5.\left(x+2\right)+\left(x+2\right)^2\right]\)
6. \(\left(x+1\right)^3+\left(x-2\right)^3\)
\(=\left[\left(x+1\right)+\left(x-2\right)\right].\left[\left(x+1\right)^2-\left(x+1\right).\left(x-2\right)+\left(x-2\right)^2\right]\)

a: \(\Leftrightarrow\dfrac{5x^2-13x+6}{A}=\dfrac{5x-3}{2x+5}\)
\(\Leftrightarrow\dfrac{5x^2-10x-3x+6}{A}=\dfrac{5x-3}{2x+5}\)
\(\Leftrightarrow A=\dfrac{\left(2x+5\right)\left(x-2\right)\left(5x-3\right)}{\left(5x-3\right)}=\left(2x+5\right)\left(x-2\right)\)
b: \(\Leftrightarrow\dfrac{x\left(x+4\right)}{A}=\dfrac{x\left(x-3\right)}{\left(x-3\right)\left(2x-1\right)}=\dfrac{x}{\left(2x-1\right)}\)
=>A=(x+4)(2x-1)

5. Ta có: a(a - 1) - (a + 3)(a + 2) = a2 - a - a2 - 2a - 3a - 6
= -6a - 6 = -6(a + 1) \(⋮\)6
<=> -6(a + 1) \(⋮\)6 \(\forall\)a \(\in\)Z
<=> a(a - 1) - (a + 3)(a + 2) \(⋮\) 6 \(\forall\)a \(\in\)Z
6. Thay x = 99 vào biểu thức A, ta có:
A = 995 - 100.994 + 100. 993 - 100.992 + 100 . 99 - 9
A = 995 - (99 + 1).994 + (99 + 1).993 - (99 + 1).992 + (99 + 1).99 - 9
A = 995 - 995 - 994 + 994 + 993 - 993 - 992 + 992 + 99 - 9
A = 99 - 9
A = 90
Vậy ....
Bài 3:
(3x-1)(2x+7)-(x+1)(6x-5)=16.
=> 6x2+21x-2x-7-(6x2-5x+6x-5)=16
=> 6x2+21x-2x-7-6x2+5x-6x+5=16
=> 18x-2=16
=> 18x=16+2
=> 18x=18
=> x=1
Bài 4:
ta có : \(n\left(n+5\right)-\left(n-3\right)\left(n+2\right)=n^2+5n-\left(n^2+2n-3n-6\right)\)
\(=n^2+5n-n^2-2n+3n+6\)
\(=6n+6=6\left(n+1\right)⋮6\)
⇔6(n+1) chia hết cho 6 với mọi n là số nguyên
⇔n(n+5)−(n−3)(n+2) chia hết cho 6 với mọi n là số nguyên
vậy n(n+5)−(n−3)(n+2) chia hết cho 6 với mọi n là số nguyên (đpcm)
Bài 6:
\(A=x^5-100x^4+100x^3-100x^2+100x-9\)
\(\Rightarrow A=x^5-\left(99+1\right)x^4+\left(99+1\right)x^3-\left(99+1\right)x^2+\left(99+1\right)x-9\)
\(\Rightarrow A=x^5-99x^4-x^4+99x^3+x^3-99x^2-x^2+99x+x-9\)
\(\Rightarrow A=\left(x^5-99x^4\right)-\left(x^4-99x^3\right)+\left(x^3-99x^2\right)-\left(x^2-99x\right)+x-9\)
\(\Rightarrow A=x^4\left(x-99\right)-x^3\left(x-99\right)+x^2\left(x-99\right)-x\left(x-99\right)+x-9\)
\(\Rightarrow A=\left(x-99\right)\left(x^4-x^3+x^2-x\right)+x-9\)
Thay 99=x, ta được:
\(A=\left(x-x\right)\left(x^4-x^3+x^2-x\right)+x-9\)
\(\Rightarrow A=x-9\)
Thay x=99 ta được:
\(A=99-9=90\)

a) Kết quả N = (x + 1)(x + 2);
b) Kết quả N = 2(x + 3)(x - 3).