Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tính chẵn lẻ:
a) TXĐ: D = R \ {π/2 + kπ| k nguyên}
Với mọi x thuộc D ta có (-x) thuộc D và
\(f\left(-x\right)=\frac{3\tan^3\left(-x\right)-5\sin\left(-x\right)}{2+\cos\left(-x\right)}=-\frac{3\tan^3x-5\sin x}{2+\cos x}=-f\left(x\right)\)
Vậy hàm đã cho là hàm lẻ
b) TXĐ: D = R \ \(\left\{\pm\sqrt{2};\pm1\right\}\)
Với mọi x thuộc D ta có (-x) thuộc D và
\(f\left(-x\right)=\frac{\sin\left(-x\right)}{\left(-x\right)^4-3\left(-x\right)^2+2}=-\frac{\sin x}{x^4-3x^2+2}=-f\left(x\right)\)
Vậy hàm đã cho là hàm lẻ
Tìm GTLN, GTNN:
TXĐ: D = R
a) Ta có (\(\left(\sin x+\cos x\right)^2=1+\sin2x\)
Với mọi x thuộc D ta có\(-1\le\sin2x\le1\Leftrightarrow0\le1+\sin2x\le2\Leftrightarrow0\le\left(\sin x+\cos x\right)^2\le2\)
\(\Leftrightarrow0\le\left|\sin x+\cos x\right|\le\sqrt{2}\Leftrightarrow-\sqrt{2}\le\sin x+\cos x\le\sqrt{2}\)
Vậy \(Min_{f\left(x\right)}=-\sqrt{2}\) khi \(\sin2x=-1\Leftrightarrow2x=-\frac{\pi}{2}+k2\pi\Leftrightarrow x=-\frac{\pi}{4}+k\pi\)
\(Max_{f\left(x\right)}=\sqrt{2}\) khi\(\sin2x=1\Leftrightarrow x=\frac{\pi}{4}+k\pi\)
b) Với mọi x thuộc D ta có:
\(-1\le\cos x\le1\Leftrightarrow-2\le2\cos x\le2\Leftrightarrow1\le2\cos x+3\le5\)
\(\Leftrightarrow1\le\sqrt{2\cos x+3}\le\sqrt{5}\Leftrightarrow5\le\sqrt{2\cos x+3}+4\le\sqrt{5}+4\)
Vậy\(Min_{f\left(x\right)}=5\) khi \(\cos x=-1\Leftrightarrow x=\pi+k2\pi\)
\(Max_{f\left(x\right)}=\sqrt{5}+4\) khi \(\cos x=1\Leftrightarrow x=k2\pi\)
c) \(y=\sin^4x+\cos^4x=\left(\sin^2x+\cos^2x\right)^2-2\sin^2x\cos^2x\)\(=1-\frac{1}{2}\left(2\sin x\cos x\right)^2=1-\frac{1}{2}\sin^22x\)
Với mọi x thuộc D ta có: \(0\le\sin^22x\le1\Leftrightarrow-\frac{1}{2}\le-\frac{1}{2}\sin^22x\le0\Leftrightarrow\frac{1}{2}\le1-\frac{1}{2}\sin^22x\le1\)
Đến đây bạn tự xét dấu '=' xảy ra khi nào nha :p

a) y' = 4x3 – 4x = 4x(x2 - 1) ; y' = 0 ⇔ 4x(x2 - 1) = 0 ⇔ x = 0, x = 1.
y'' = 12x2 - 4 .
y''(0) = -4 < 0 nên hàm số đạt cực đại tại x = 0, ycđ = y(0) = 1.
y''(1) = 8 > 0 nên hàm số đạt cực tiểu tại x =
1, yct = y(
1) = 0.
b) y' = 2cos2x - 1 ;
y'' = -4sin2x .
nên hàm số đạt cực đại tại các điểm x =
+ kπ, ycđ = sin(
+ k2π) -
- kπ =
- kπ , k ∈ Z.
nên hàm số đạt cực tiểu tại các điểm x =
+ kπ, yct = sin(
+ k2π) +
- kπ =
- kπ , k ∈ Z.
c) y = sinx + cosx = ; y' =
;
![]()
Do đó hàm số đạt cực đại tại các điểm , đạt cực tiểu tại các điểm
d) y' = 5x4 - 3x2 - 2 = (x2 - 1)(5x2 + 2) ; y' = 0 ⇔ x2 - 1 = 0 ⇔ x = ±1.
y'' = 20x3 - 6x.
y''(1) = 14 > 0 nên hàm số đạt cực tiểu tại x = 1, yct = y(1) = -1.
y''(-1) = -14 < 0 hàm số đạt cực đại tại x = -1, ycđ = y(-1) = 3.










a) y = sin2x
Hàm số có chu kỳ T = π
Xét hàm số y=sin2x trên đoạn [0;π], ta có:
y' = 2cos2x
y' = 0 ⇔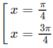
Bảng biến thiên:
Do đó trên đoạn [0;π] , hàm số đạt cực đại tại π/4 , đạt cực tiểu tại 3π/4 và y C D = y(π/4) = 1; y C T = y(3π/4) = −1
Vậy trên R ta có:
y C Đ = y(π/4 + kπ) = 1;
y C T = y(3π/4 + kπ) = −1, k∈Z
b) Hàm số tuần hoàn chu kỳ nên ta xét trên đoạn [−π;π].
y′ = − sinx – cosx
y′ = 0 ⇔ tanx = −1 ⇔ x = −π4 + kπ, k∈Z
Lập bảng biến thiên trên đoạn [−π;π]
Hàm số đạt cực đại tại x = −π4 + k2π , đạt cực tiểu tại x = 3π4 + k2π (k∈Z) và
y C Đ = y(−π4 + k2π) = 2 ;
y C T = y(3π4 + k2π) = − 2 (k∈Z).
c) Ta có:
Do đó, hàm số đã cho tuần hoàn với chu kỳ π.
Ta xét hàm số y trên đoạn [0;π]:
y′ = sin2x
y′ = 0 ⇔ sin2x = 0 ⇔ x = kπ/2 (k∈Z)
Lập bảng biến thiên trên đoạn [0,π]
Từ đó, ta thấy hàm số đạt cực tiểu tại x = kπ/2 với k chẵn, đạt cực đại tại x = kπ/2 với k lẻ, và
y C T = y(2mπ) = 0; yCT = y(2mπ) = 0;
y C Đ = y((2m+1)π/2) = 1 (m∈Z)