PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 4 2016
Ta có : \(y'=3x^2-6x+m^2\Rightarrow y'=0\Leftrightarrow3x^2-6x+m^2=0\left(1\right)\)
Hàm số có cực trị \(\Leftrightarrow\left(1\right)\) có 2 nghiệm phân biệt \(x_1;x_2\)
\(\Leftrightarrow\Delta'=3\left(3-m^2\right)>0\Leftrightarrow-\sqrt{3}< m< \sqrt{3}\)
Phương trình đường thẳng d' đi qua các điểm cực trị là : \(y=\left(\frac{2}{3}m^2-2\right)x+\frac{1}{3}m^2\)
=> Các điểm cực trị là :
\(A\left(x_1;\left(\frac{2}{3}m^2-2\right)x_1+\frac{1}{3}m^2+3m\right);B\left(x_2;\left(\frac{2}{3}m^2-2\right)x_2+\frac{1}{3}m^2+3m\right);\)
Gọi I là giao điểm của hai đường thẳng d và d' :
\(\Rightarrow I\left(\frac{2m^2+6m+15}{15-4m^2};\frac{11m^2+3m-30}{15-4m^2}\right)\)
A và B đối xứng đi qua d thì trước hết \(d\perp d'\Leftrightarrow\frac{2}{3}m^2-2=-2\Leftrightarrow m=0\)
Khi đó \(I\left(1;-2\right);A\left(x_1;-2x_1\right);B\left(x_2;-2x_2\right)\Rightarrow I\) là trung điểm của AB=> A và B đối xứng nhau qua d
Vậy m = 0 là giá trị cần tìm
NM
1
16 tháng 10 2015
ta tính \(y'=\frac{x^2+1-2x^2}{\left(x^2+1\right)^2}=\frac{1-x^2}{\left(x^2+1\right)^2}\)
ta giải phương trình y'=0
suy x=1;x=-1
ta tính \(y''=\frac{-2x\left(x^2+1\right)^2-4x\left(x^2+1\right)\left(1-x^2\right)}{\left(x^2+1\right)^4}=\frac{-2x\left(x^2+1\right)-4x\left(1-x^2\right)}{\left(1+x^2\right)^3}=\frac{2x^3-6x}{\left(1+x^2\right)^3}=\frac{-2x\left(x^2+2\right)}{\left(1+x^2\right)^3}\)
ta có \(y''\left(1\right)=-3<0\)hàm số đạt cực đại tại x=1
\(y''\left(-1\right)=3>0\)hàm số đạt cực tiểu tại x=-1
27 tháng 3 2016
Hàm số có cực đại, cực tiểu khi m<2. Tọa độ các điểm cực trị là :
\(A\left(0;m^2-5m+5\right);B\left(\sqrt{2-m};1-m\right);C\left(-\sqrt{2-m};1-m\right)\)
23 tháng 4 2016
Ta có : \(y'=4x^3+12mx^2+6\left(m+1\right)x=2x\left(2x^2+6mx+3\left(m+1\right)\right)\)
\(\Rightarrow y'=0\Leftrightarrow x=0\) hoặc
\(\Leftrightarrow f\left(x\right)=2x^2+6mx+3m+3=0\)
a) Hàm số có 3 cực trị khi và chỉ khi \(f\left(x\right)\) có 2 nghiệm phân biệt khác 0
\(\Leftrightarrow\begin{cases}\Delta'=3\left(3m^2-2m-2\right)>0\\f\left(0\right)\ne0\end{cases}\)\(\Leftrightarrow\begin{cases}m< \frac{1-\sqrt{7}}{3}\cup m>\frac{1+\sqrt{7}}{3}\\m\ne-1\end{cases}\)
b) Hàm số chỉ có cực tiểu mà không có cực đại
\(\Leftrightarrow\) hàm số không có 3 cực trị \(\Leftrightarrow\frac{1-\sqrt{7}}{3}\le m\le\frac{1+\sqrt{7}}{3}\)
Hàm số xác định và có đạo hàm với mọi x ≠ 1.
y′=0 ⇔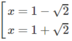
Bảng biến thiên:
Hàm số đạt cực đại tại x = 1 − 2 và đạt cực tiểu tại x = 1 + 2 , ta có:
y CD = y(1 − 2 ) = −2 2
y CT = y(1 + 2 ) = 2 2